Venn Diagrams

• Venn diagrams are a way to visualize sets.
• They were formalized by John Venn (1834-1923)
• (wikipedia)
• In a Venn diagram
  • A square represents the universal set.
  • A circle represents some (perhaps improper) set of the universal set.
• Draw a Venn diagram to represent U={1,2,3,4,5,6,7,8,9}, A={1,3,5,7,9}
• When we have two sets (A,B) , we have four cases
  • A=B
  • A &issub; B
  • A and B are disjoint or have no elements in common
  • A ⊄ B and B⊄ A, but for some x, x∈ A and x∈ B
• For three sets this is much more complex.
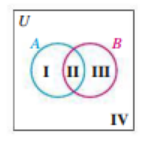
• What do the regions of this represent?
  • 
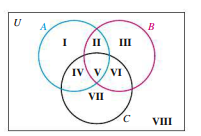
• What do the regions of this represent?
  • 
• The complement of a set A, written A', is the set of all elements in the Universial set U that are not in A.
  • U={1,2,3,4,5,6,7,8,9}, A={1,3,5,7,9}, find A'
• The intersection of two sets A and B, written A ∩ B, is the set containing all elements in both set A and in set B.
  • U={1,2,3,4,5,6,7,8,9}, A={1,3,5,7,9}, B = {1,2,3,4,5} find A ∩ B
• The union of two sets, written A ∪ B, is the set containing all elements in set A or set B or both.
  • U={1,2,3,4,5,6,7,8,9}, A={1,3,5,7,9}, B = {1,2,3,4,5} find A ∪ B
• Normally union means or and intersection means and.
• n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
• Do some problems
  • 15
  • 23-28
  • 29-34
  • 35-42
  • 93-94