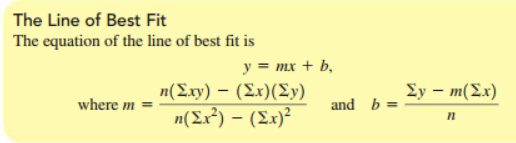12.6 Linear Correlation and Regression

• I think that attendance in class and grades are related.
  • Mathematically what I am saying is that they are Correlated
  • Notice I did not say missing classes causes lower grades.
  • People may not attend class for many reasons.
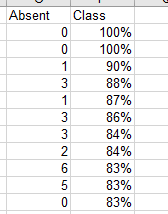
• I have two pieces of information for each student that I want to look at
  • The first is the total number of absences.
  • The second is the class score.
  • A screen shot of part of the data:
  • 
  • 
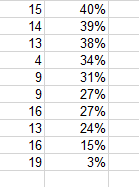
  • Summary statistics
  • 
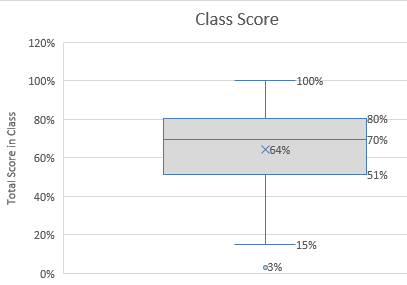
• Sometimes it is helpful to draw a Box and Whisker Plot
  • In this picture, the Min-Max is displayed
  • As well as any outliers or extreme data.
  • 
  • 
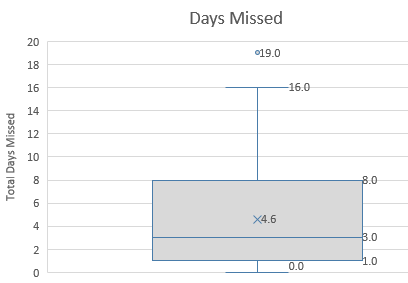
  • In both cases it looks like 19 days missed with 3% is an outlier
• We want to identify an independent and a dependent variable.
  • The independent variable is something we have control over.
  • The dependent variable is something that depends on the independent variable.
  • In this case, we assume the student has control over the number of days absent, so this is the independent variable.
• A scatter plot or scatter diagram gives us an indication of how the data is related
  • Plot the independent variable on the x axis
  • Plot the dependent variable on the y axis.
  • 
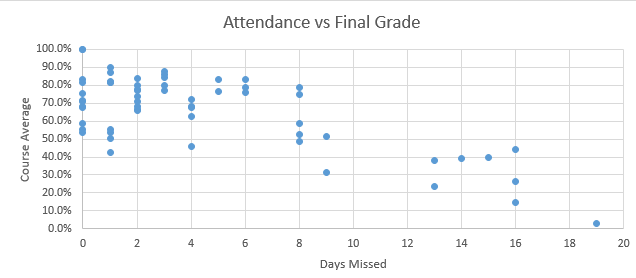
  • Even with the outlier, it looks like there is a relationship
    • As days missed goes up, the class average goes down.
    • This is an inverse relationship.
    • Or a negative correlation
  • The question is, could we draw a "line" that approximated the data?
  • 
• Here are some scatter plots from the book
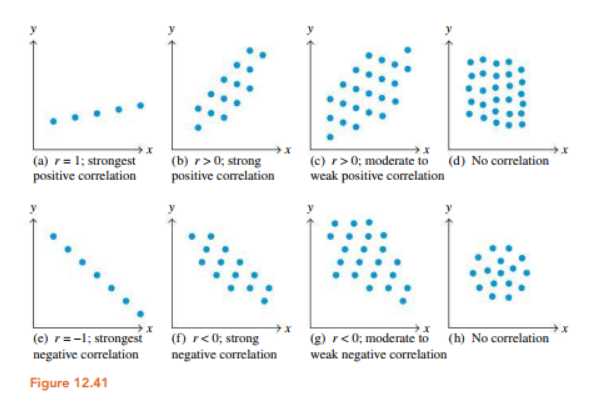
• But what is this r value?
  • $r=\frac{n(\Sigma xy) - (\Sigma x) (\Sigma y)}{\sqrt{n(\Sigma x^2)-(\Sigma x)^2} \sqrt{n(\Sigma y^2) - (\Sigma y)^2}}$
  • r is called the correlation coefficient
  • You can build this in a table.
  • But for any real data set you should use software.
  • For our data the value is -.71
• correlation coefficient
  • 1 means correlation
  • -1 means negative correlation
  • 0 means no correlation.
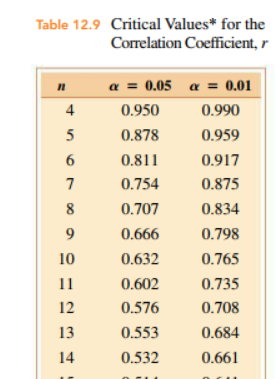
• There are ways to test to see if the correlation is "significant" or what is the likelihood that something identified as a correlation is in error.
  • In general it depends on the amount of data and the probability of error.
  • 
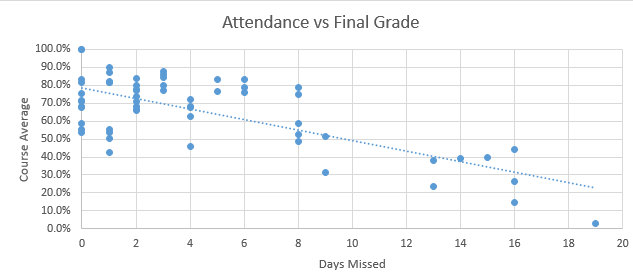
• There are also formulas for computing the line of best fit.
  • 
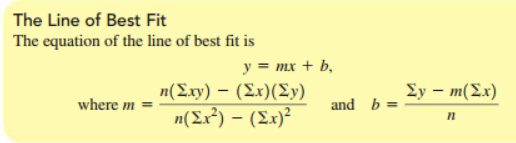
  • You can ask excel to display this for you.
  • 
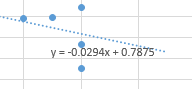
  • For data in the range (0 ≤ days missed ≤ 19) you can use this equation to estimate the class grade.