The Normal Curve

• Think about different types of histograms we might get from different types of data
• The Uniform Distribution.
  • 
  • 
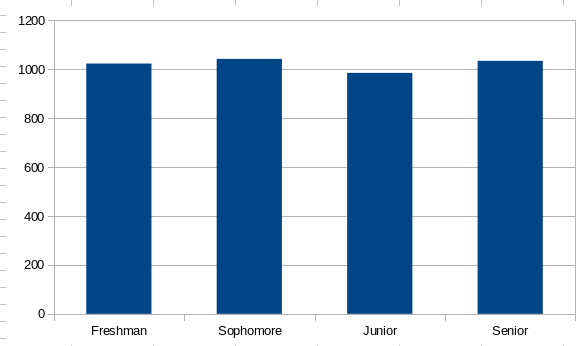
  • All of the classes tend to have the same count.
  • This is true when the population is very uniform
• J shaped distribution
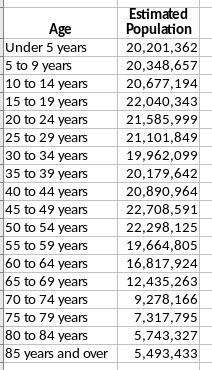
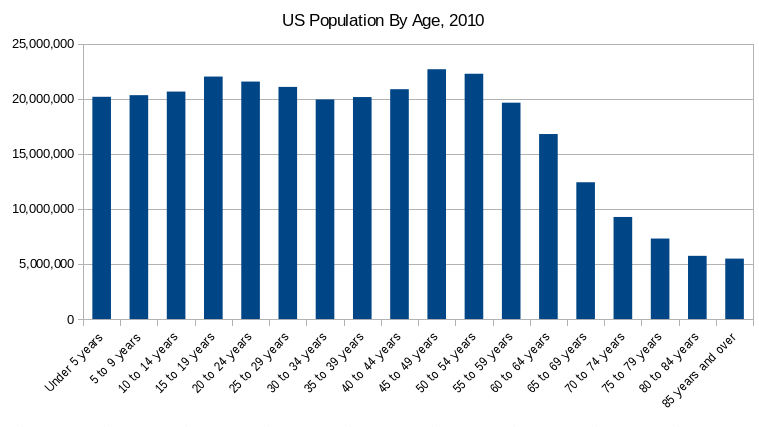
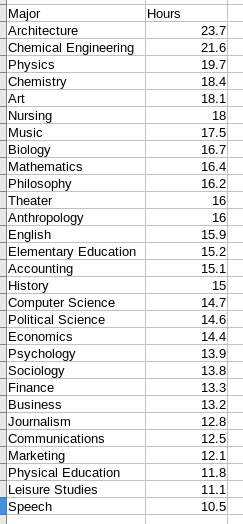
  • I found this article on hours spent studying per week in 2011.
  • 
  • 
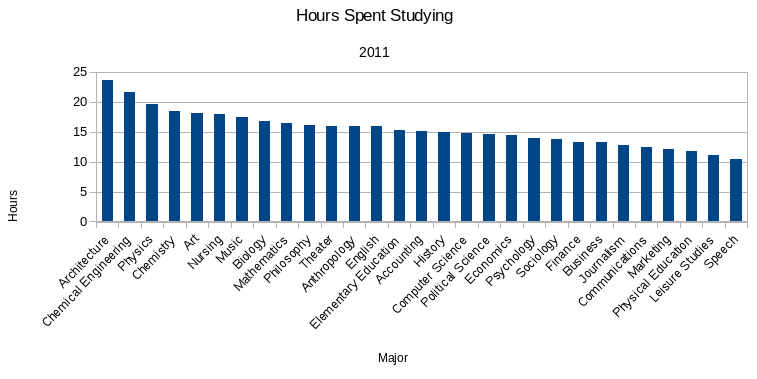
  • This happens with things like studying where people get to choose how much time to invest in something.
• Bi-modal
  • This is from the Census
  • 
  • 
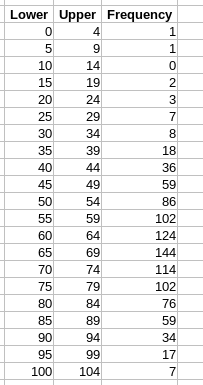
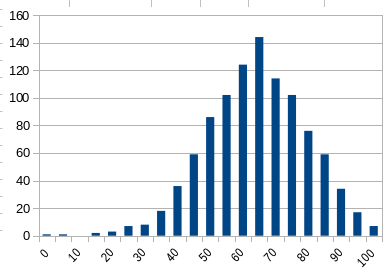
• Normally distributed data
  • Scores on Math Tests in the US from kaggle.com
  • 
  • 
• There are many cases where data fits
• As we add more categories, these graphs tend to become more smooth and we usually represent them as lines, not columns.
• Draw each.
• The normal distribution is interesting
  • Called the Gaussian Distribution because it was studied by may 8^th great ancestor Carl Friedrich Gauss
  • 
  • The graph is called the bell curve
  • The mean median and mode are all the same in the normal distribution.
  • The data is symmetrically distributed about the mean.
• There are many things that occur naturally in the world that are normally distributed or approximately normally distributed.
  • Size things like height and weight.
  • Other natural abilities like IQ (cringe)
  • Duration things like the life of a set of tires.
• It is so frequent that we will study this distribution.
• The Empirical Rule states
  • About 68% of the population lies within one standard deviation of the mean.
  • About 95% of the population lies within two standard deviations of the mean.
  • About 99.7% of the population lies within three standard deviations of the mean.
• Given the mean (μ) and standard deviation (σ) of a population that is normally distributed, we can decide what percent of the population has a given value.
• To do this
  • We compute something called the z-score
  • Based on the z-score we can find the percent of the population to the left of the z-score based on the Areas of a Standard Normal Distribution table.
  • Finally we will do some geometric reasoning we will be able to describe other facts about the data.
• z-score
  • For a given piece of data x, $z_x=\frac{x-\mu}{\sigma}$
• Do problems Page 779 on