Installment Buying (Fixed)

• In this type of loan, the borrow agrees to pay a fixed number of payments which include principal and interest.
• This is not a simple interest loan.
• The terms of the loan include
  • The principal or amount borrowed
  • The interest rate
  • The time.
  • The number of payments per year.
• Examples of this type of loan include car loans, student loans, ...
  • Any loan where you make a set number of regular payments.
• These do not include credit cards, as credit cards are open installment loans.
• The steps in these loans depend on the question.
  • Sometimes you are asked to compute a down payment
  • Sometimes you are asked to compute the amount financed which is the price - down payment.
  • You normally need to compute the finance charge, which is the total amount of money the borrower must pay for using the principal.
  • Sometimes you need to compute the monthly payment.
• Finance charges can be computed two ways
  • The Installment payment formula $$m = {p ({r \over n}) \over 1 - ( 1 + { r \over n}) ^ (-nt)}$$
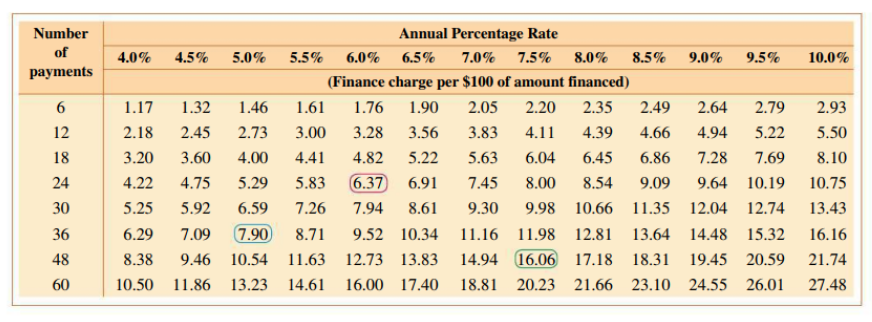
  • Or use the Annual Percentage Rate Table for Monthly Payment Plans
    • 
  • I think, for our purposes, the second is easier.
• Do 7-10 page 602
• Do 11 or 12
• Sometimes you need to work backwards
• look at 13-16.
• Sometimes you want to pay off a loan early
  • You need to compute unearned interest or interest that you don't need to pay
  • $ u = {n p V \over 100+V} $
  • u is unearned interest
  • n is the number of payments remaining
  • p is the monthly payment
  • V is lookup n and r on the chart
  • Payoff = this month + remaining months - unearned interest
  • $ payoff = p + np -u $
• Look at 17-20