Euler Diagrams and Syllogistic Arguments.

• Based on Aristotle's work.
• We are concerned with the statements
  • All _____ are _____
  • No _____ are _____
  • Some _____ are _____
  • Some _____ are not _____
  • _____ is a _____
  • _____ is not a _____
• All doctors are tall, Maria is a doctor, therefore Maria is tall.
  • Draw a box to represent the world of people
  • Draw a circle to represent tall people.
  • Draw a circle to represent doctors. (Inside the set of tall)
  • Now place a square, to represent Maria, where it must be, but contrary to the conclusion if possible.
  • So in this case, the square must be inside of the doctor circle, so it must be inside of the tall circle.
  • Since we can't place the square outside of the tall circle, the argument is valid.
  • 
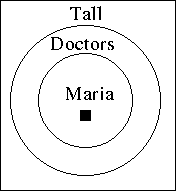
• This diagram is called an Euler Diagram.
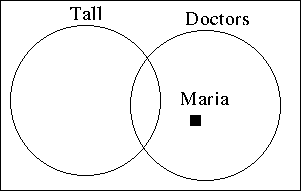
• Some doctors are tall, Maria is a doctor, therefore Maria is tall
  • In this case, since some doctors are tall, we can argue some are not.
  • So the circles intersect, but are not contained.
  • And we can place Maria in the not tall doctor set without violating a premise
  • So the conclusion is not valid.
  • 
• No doctors are tall, Maria is not a doctor, therefore Maria is not tall
  • The two circles do not overlap
  • Maria must be placed outside of the doctor set.
  • But she can easily be placed inside of the tall set.
  • Therefore the conclusion is not valid.
  •