The Normal Curve

• If we draw histograms for different data sets, we start to see some patterns arise.
• Draw a histogram for rolling a 6 sided die
  • I rolled a six sided die 500 times.
  • 
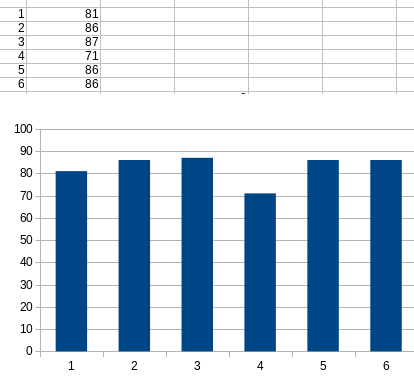
  • What would happen as we tossed more and more dice?
  • What would happen as we let the number of sides increase?
  • This is an example of a rectangular or uniform distribution.
• There are many other shapes that occur
• A Poisson distribution describes cars arriving at a traffic light in a small town.
  • 
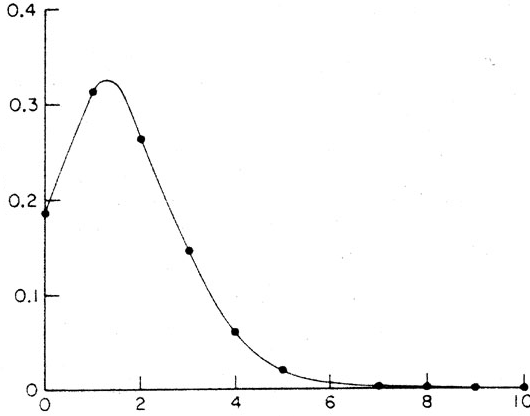
  • This is an example of a J shaped distribution
  • It is also skewed to the right.
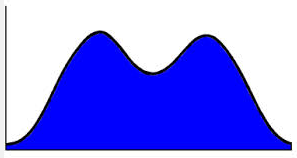
• Grades tend to be in a bimodal distribution
• 
• The normal distribution
  • Also known as the Gaussian distribution
  • Or the bell curve
  • We believe that many of the populations occurring in this world follow the normal distribution.
  • Or closely related to the normal distribution.
• In a population that is normally distributed
  • The mean, median and mode are all the same.
  • The population is symmetrically distributed about the mean
• If we know that a population is normally distributed then
  • If we know the mean and the standard deviation, we can predict how much of the population is in a given position.
• The Empirical Rule states that
  • For a normally distributed population,
  • Approximately 68% of the data lies within one standard deviation of the mean.
  • Approximately 95% of the data lies within two standard deviations of the mean
  • Approximately 99.7% of the data lies within three standard deviations of the mean
• Police officer's salaries are normally distributed with a mean of $50,000 and a standard deviation of $7,000.
  • Calculate σ +/- μ, σ +/- 2μ, σ +/- 3μ
  • What percent of police officers have a salary less than $50,000
  • What percent of police officers have a salary greater than $50,000
  • Between $43,000 and 57,000
  • Less than $43,000
  • More than $64,000
  • More than $71,000
• If we want to deal with fractions of a standard deviation, we do the same thing but with a z score
• The z score for some data x

  
       x-μ
  zx = ---
        σ
        

• Looking at z_x
  • If it is negative, then x < μ
  • If it is positive, then x > μ
• The tables on page 822, 823 give us the area (or percent of the population) to the left of any given z score.
• Examples:
  • z_x = 0.71, find the percent of the population less than x, greater than x, between μ and x
  • z_x = -2.18, z_y = -1.90. Find the percent of the population between x and y, less than x and greater than y.
• A vending machine is designed to dispense a mean of 7.6 oz of coffee into an 8 oz cup. If the amount of coffee dispensed is normally distributed, with a standard deviation of 0.4oz. find the percent of time that the machine will
  • Dispense between 7.4 and 7.7 oz.
  • Dispense less than 7.0 oz
  • Dispense less than 7.8 oz
  • Overflow the cup.
• Assume that the speed of automobiles on an expressway during rush hour is normally distributed with a mean of 62mph and a standard deviation of 5mph.
  • What percent of cars are traveling at or below 62mph
  • What percent are traveling between 58mph and 66mph
  • What percent are traveling faster than 70mph
  • If 200 cars are traveling down the road, how many will be traveling 70mph or faster.