Tree Diagrams

The Fundamental Counting Principle: If one experiment can be performed m ways (has m outcomes) and another can be performed n ways (has n outcomes) then the two experiments, in that order, can be performed m×n ways.
How many outcomes are in the experiment roll a die then toss a coin?
- There are 6 outcomes from rolling a die.
- There are two outcomes from tossing a coin
- So there are 6× 2 or 12 outcomes from combining the two.
We can draw such an experiment with a tree diagram
- This is just an easy way to explore the sample space
- List all of the outcomes for experiment 1
- List all the outcomes for experiment 2 for each outcome of experiment one
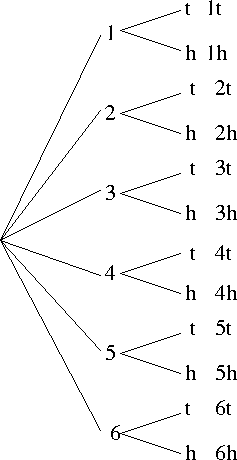
- This is probably not effective for very large sample spaces.
The probability of an even happening at least once is given by
- P(even happening at least once) = 1-P(even does not happen)
If an experiment on a set of items is conducted twice it can be conducted
- Without replacement: the item selected is not returned to the pool
- With replacement: the item is returned to the pool.
Exercises
A box contains six calculators, all the same size, but each a different color. Two calculators are selected. What is the size of the sample space
- With Replacement
- Without replacement.
- Two coins are tossed.
  - Find the points in the sample space.
  - Find the probability that
    - No heads are tossed
    - At least one head is tossed
    - Exactly One head is tossed
    - The two values are the same
- A couple plans on having three children.
  - Find the size of the sample space.
  - Find the points in the sample space
  - Find the probability that
    - No children are boys
    - At least one child is a boy
    - All three children are boys
    - All three children are the same gender.
- Two dice are rolled
  - How many points in the sample space?
  - Find the probability of
    - A double
    - the sum is 8
    - A 2 is rolled
    - A 2 is not rolled
    - At least one two is rolled.