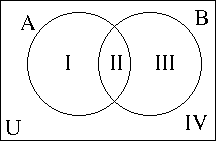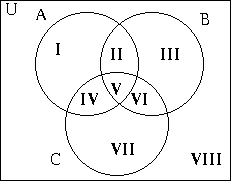Venn Diagrams and Set Operations

• Venn diagrams provide a way to visualize sets.
• Consider a set A, A ⊆ U
  • All of the elements of A are in U, but there might be some that are not.
  • We draw this picture.
  • 
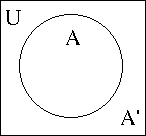
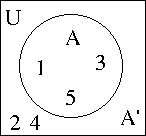
  • All items under consideration are in the universal set U.
  • The items inside of the circle are in set A.
  • The items outside of the circle are in U but not in A, or the complement of A written A'
  • Example: U = { 1,2,3,4,5}, A = { 1, 3, 5} , A' = { 2, 4}
  • 
• Consider the relationship between two sets A and B, A⊆ U, B ⊆U.
  • If A=B, we have the case above.
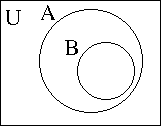
  • If A ⊂ B, we have
  • 
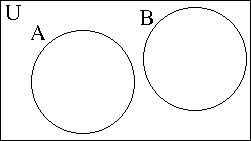
  • If A and B have no elements in common, they are disjoint
  • 
  • The common assumption is to assume that A⊄B and B⊄A, but there are some elements in common.
  • 
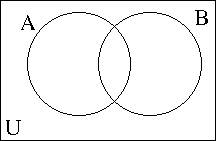
    • This breaks the Universal set into four regions.
    • We number these with roman numeral I, II, III, IV
    • 
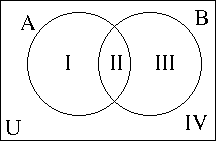
    • I contains elements in A, but not in B.
    • II contains the elements common to A and B
    • III contains elements in B but not in A.
    • IV contains elements that are not in A or in B.
    • Example: U = { 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8}
    • 
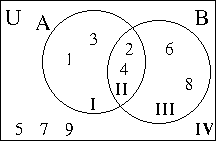
    • I will define n(I) to be the number of elements in region I
    • n(A) = 4, n(I) = 2, n(II) = 2, n(III) = 2, n(IV) = 3
    • Note that n(A) = n(I) + n(II), n(B) = n(II) + n(III)
  • Some set operations:
    • Operations on integers are +, -, / and ×
    • Complement
      • As described above, this is the set of the elements of U not in A
    • Intersection
      • The intersection of two sets A, B, written A∩B is a set containing all elements that are in both A and B
      • This is region II above.
      • So from the previous example A∩B = { 2, 4}
      • This is usually "and" in English.
    • Union
      • The union of two sets A and B, written A∪B is the set of all elements x, where x∈A or x∈B (or both)
      • This is regions I, II, and III above
      • A∪B = { 1,2,3,4,6,8}
      • This is usually or in English.
    • For finite sets n(A∪B) = n(A) + n(B) - n(A∩B)
    • Difference
      • The difference between two sets A and B, written A-B is the set of elements in set A but not in set B.
      • A-B above = {1,3}
• Examples: 21 through 26, 33 through 40, 41 through 48, 49 through 58, 100

Venn Diagrams with Three Sets

• With three sets, Venn diagrams become somewhat more complex.
• 
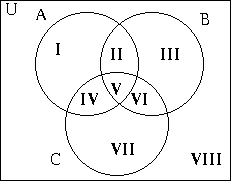
• Roman numerals I through VIII
• n(A) = n(I) + n(II) + n(IV) + n(V)
• n(A∪B) = n(A)+n(B)-n(A∩B)
• n(A∪B∪C) = n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩B∩C)
• Examples 9, 11, 15, 17