Venn Diagrams and Set Operations

• Venn diagrams are useful for picturing the relationship between sets.
• Especially for one, two or three sets.
• A set is normally represented as a circle.
• The universal set is a rectangle.
• The compliment of a set A, A' are all the elements in the Universal set not in A.
• Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10}
• Let A = { 2, 4, 6, 8}
• A' = { 1, 3, 5, 7, 9, 10}
• 
• Venn diagrams of two sets.
  • A = B
  • 
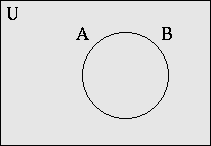
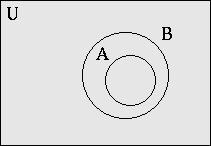
  • A ⊂ B
  • 
  • No items in common
  • 
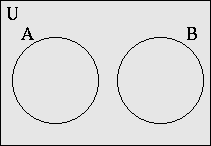
  • Some items in common, but A⊄B, B⊄A
  • 
• The intersection of two sets A and B is the set of items that are in both.
• B = { 6, 7, 8, 9, 10}
• A ∩B = { 6, 8}
• This is represented by region II
• The union of two sets A and B is the set of all items that are elements of A or of B.
• A ∪B = { 2, 4, 6, 7, 8, 9, 10}
• n(A∪B) = n(A) + n(B) - n(A∩B)
• The difference of two sets A-B is the set of elements of A not in B.
• A-B = { 2, 4 }
• This is region I
• In problems, and usually means intersection (did both)
• In problems, or usually means union (did one or the other or both)
• Example Problem 100

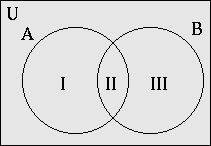
  Let U = { All students at Henniger High School}
  Let B = { All students in the band}
  Let C = { All students in the Chorus}
  
  n(B∪C) = 46
  n(B) = 30
  n(B∩C) = 4
  
  We know n(B∪C) = n(B) + n(C) - n(B∩C)
             46      = 30   + x   - 4
  
     

Venn diagrams with three sets

• 
• n(A∪B∪C) = n(A) + n(B) + n(C) - n(A∩B) - n(A∩C) - N(B∩C)+2n(A∩B∩C);

Homework

• Page 69, 21 to 71 odd
• Page 77, 9 to 59 odd