Sets continued.

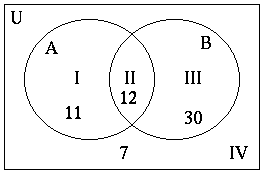
• If we conduct a survey of 60 people
  • We find that :
    • 42 of them like to go to movies
    • 23 of them like to go dancing
    • and 12 of them like to do both.
  • Then can we figure out:
    • How many like dancing but not movies
    • How many like movies but not dancing
    • How many don't like either.

    Let A be the set of people who like the movies
    Let B be the set of people who like dancing.
    
    We know n(A) = 42 
            n(B) = 23 
    	n(U) = 60
    	n(II) = 12
    
    n(I) = n(A) - n(II) 
         = 42 - 12 = 30 
    
    n(II) = n(B) - n(II) 
          = 23 - 12
          = 11 
    
    So the number of people who like movies, dancing or both is
         n(I) + n(II) + n(III) 
        = 30 + 12 + 11 
        = 53
    So the number who don't like either are
        n(U) - (n(I)+n(II) + n(III))
        = 60 - 53
        = 7
    
        
           

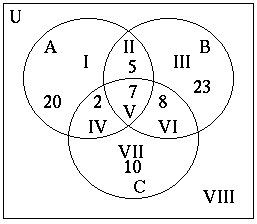
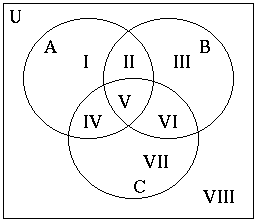
• When we have three sets, things get a bit more complicated.
  • We usually have more information.
    • The number of people in each set
    • The number of people in all three sets
    • The number of people in any two sets.
    • Example: 100 people were asked how they spent their evening
      • 34 said that they studied
      • 43 said that they watched tv
      • 27 said that they chatted with friends
      • 7 said that they did all three
      • 12 said that they watched tv and studied
      • 9 said that they chatted and studied
      • 15 said that they chatted and watched tv
    • In this case, let:
      • A be the set of people who studied
      • B be the set of people who watched tv
      • C be the set of people who chatted with friends
  • The Venn Diagram is somewhat more complex as well.
    • 
  • What is represented by region V?
    • Notice that V is in all three sets
    • So it represents people who did all three things.
    • so n(V) = 7
  • What does II represent
    • It is in set A, so they studied
    • It is also in set B, so they watched TV
    • But it is not in set C, so they did not chat with friends.
    • Is this the 12 who said that they studied and watched tv?
      • No, that could include people who chatted as well.
      • So the 12 who said they studied and watched tv
    • So II is really the set who studied and watched TV, but did not chat with friends.
  • What represents the 12 people who studied and watched tv?
    • That would be everywhere that A and B intersect.
    • So that would be II and V
    • n(II) + n(V) = 12
  • So we can then figure out how many studied and watched tv, but did not chat with friends n(II)
    • This is just algebra.

       n(II) + n(V) = 12
       n(II)        = 12 -n(V)
      	      = 12 - 7
      	      = 5
      		

• We can do the same for IV

         (people who studied and chatted with friends)
  n(IV) + n(V) = 9 
  n(IV) = 9 - n(V)
        = 9  -7 
        = 2
         

• And now we can find n(I)

  n(A) = n(I) + n(II) + n(IV) + n(V)
  34 = n(I) + 5 + 7 + 2
  34 = n(I) + 14
  34-14 = n(I)
  n(I) = 20 
  
  so 18 people only studied
         

• VI can be dealt with as well.

  n(VI) + n(V) = 15
  n(VI) = 15 - n(V) 
        = 15 - 7
        = 8
         

• And to finish

  n(III) = n(B) - (n(II)  + n(V) + n(VI))
         = 43 - (5 + 7 + 8) 
         = 43 - 20 
         = 23
  
  n(VII) = n(C) - (n(IV) + n(V) + n(VI))
         = 27 - (2 + 7 + 8)
         = 27 - 17
         = 10
  
  n(VIII) = n(U) - (n(I) + n(II) + n(III) + n(IV) + n(V) + n(VI) + n(VII))
          = 100 - (20 + 5 + 23 + 2 + 7 + 8 + 10) 
  	= 100 - 75
  	= 25
         

  

Homework