Sets
A Set is a collection of objects
These objects are called elements
Sets can be listed using a roster method
A = {Red, Green, Blue, Cyan, Magenta, Yellow}
Sets can also be listed using a description
A is the set of all people who live in Pennsylvania.
When discussing several related sets, the universal set
is the set that contains all elements under discussion.
Set A is a subset of set B if all elements in set A are
also members of set B.
Example:
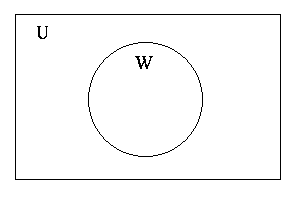
Let U be the set of all people in this room
Let W be the set of all women in this room
W is a subset of U
Is U a subset of W?
Can we construct an example where this is true?
We can draw a picture of sets, we call this a Venn Diagram
Draw a rectangle to represent the universal set, label this U.
Draw a circle to represent each subset, label these appropriately
and write the description of the set.
 Sometimes we deal with multiple sets from the same universal set.
Let J be the set of all people in the room who work.
If the two sets can possibly have some elements in common, we draw
the circles with some common area.
Sometimes we deal with multiple sets from the same universal set.
Let J be the set of all people in the room who work.
If the two sets can possibly have some elements in common, we draw
the circles with some common area.
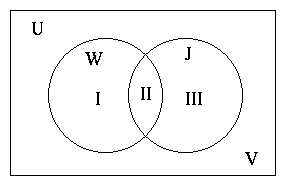 Notice I have also numbered this Venn Diagram.
Notice I have also numbered this Venn Diagram.
- I represents the set of women without jobs
- II represents the set of women who have jobs
- III represents the set of those who have jobs who are not women.
- V represents the set of people who are not women and do not have jobs.
II is called the intersection of the two sets, it is described by the word and. "Those who are women and have jobs"
This is represented by W ∩ J
Notice that II can be empty (A = set of men, B = set of women, A and B is empty)
I and II and III represent the union of two sets.
W ∪ J is the symbol for union and represents elements common to both.
if A is a set n(A) is an operation that tells us the number of elements in A.
Example
Let A be the set of positive numbers less than 5
Let B be the set of even numbers less than 11
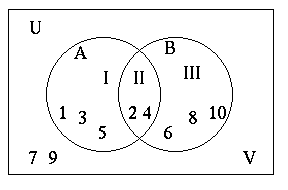 what is:
n(A)? A={1,2,3,4,5} so n(A) = 5
n(B)? B={2,4,6,8,10} so n(A) = 5
n(A ∩ B) or n(II)?
II = {2,4} so n(II) = 2
n(I) = 3
n(III) = 3
n(IV) = 2
n(U) = 10
what is:
n(A)? A={1,2,3,4,5} so n(A) = 5
n(B)? B={2,4,6,8,10} so n(A) = 5
n(A ∩ B) or n(II)?
II = {2,4} so n(II) = 2
n(I) = 3
n(III) = 3
n(IV) = 2
n(U) = 10
Example:
A survey of 20 people finds that
8 people have dogs,
7 people have cats
and 3 people have both dogs and cats.
How many people have just dogs?
How many people have just cats?
How many people have neither cats or dogs?
n(A) = 8
n(II) = 3
n(I) = n(A)-n(II)
n(I) = 8-3 = 5
n(B) = 7
n(II) = 3
n(III) = n(B)-n(II) = 7-3 = 4
n(I) + n(II) + n(III) = 5 + 3 + 4 = 12
n(V) = n(U)- n(I) + n(II) + n(III)
= 20-12 = 8
Do problem 10, page 80
Homework
Do 1-8 all page 80


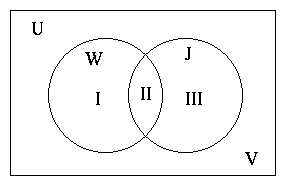
what is: n(A)? A={1,2,3,4,5} so n(A) = 5 n(B)? B={2,4,6,8,10} so n(A) = 5 n(A ∩ B) or n(II)? II = {2,4} so n(II) = 2 n(I) = 3 n(III) = 3 n(IV) = 2 n(U) = 10