Beginning the Analysis Phase.

• Today we will work with the superhero dataset
• We will apply some basic statistics functions.
  • I will discuss these as we compute them.
  • Please help out.
  • If you have not had a stats class, please ask if you don't understand what we are computing.
• Make a copy of the Raw Data tab, call it Working Data
• Let's name the fields in the working data tab.
  • On the Working Data worksheet select the entire data range.
  • On the Formulas tab in the Defined Names select Create from Selection
  • Make sure that top row is the only thing selected.
  • Press OK.
• Check your new names by clicking on the Name Manager in the same area
  • If the scope of the name is workbook, it is available everywhere.
  • If you set the scope to be worksheet, this will only be available in the worksheet.
  • Be careful not to define the same name twice.
• Let's start by analyzing the Height field.
  • Add a new tab, label this Height
  • In A1 put: This worksheet provides a basic analysis of the height field.
• Counting the field is sometimes helpful
  • At this stage it will let us know if all of the data is valid
  • Move to the Height worksheet.
  • In A5 put Numeric
  • In B5 put =count(height)
  • Did this computation do what you expected?
    • What did you expect?
    • What did it produce?
    • How do we know this is valid?
  • There are a few other count functions I would like you to do
    • In A3 put Counts
    • Merge this across A3:B3
    • In A4 put All
    • In B5 put =counta(height)
    • There doesn't seem to be a difference here.
      • Add a sandbox tab.
      • In A1:a3 put 1, 2, 3
      • An A4:A6 put a, b, c
      • In A8 put NA
      • In A9 put na (lower case)
      • 
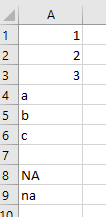
      • Name A1:A9 as list1
        • Use the define name selection in the name manager
        • Set the scope to be sandbox
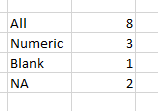
      • Do a count, counta on list1
      • Add a =countblanks(list1)
      • Add a cell called NA, then =countif(list1, "na"), or better yet, reference the cell.
      • 
      • 
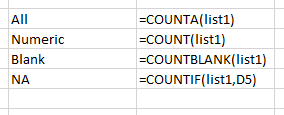
      • What information can we gather from these four counts?
    • Return to the Height worksheet and add the other two counts.
    • In every stats class you discuss the "measures of central tendency"
      • What are these?
        • Mean
        • Median
        • Mode
        • Midrange
      • Mean
        • This is what is generally meant by "average".
        • Add up all of the numbers and divide by the number of numbers.
        • Should we use the formula?
        • Ok in cell A9 put Mean
        • In B9 put =average(height)
        • What does this tell us?
        • Is this what we expect?
        • Let's go back to the sandbox
          • Find the average of list1.
          • What happened to the other values?
          • Change the value in cell A1 to be 10000
          • What happened to the mean?
          • Outliers change the mean?
      • The median is the middle number
        • Sort the numbers and find the one in the middle.
        • The formula =median(height) will calculate the median
        • Is there anything strange about these results?
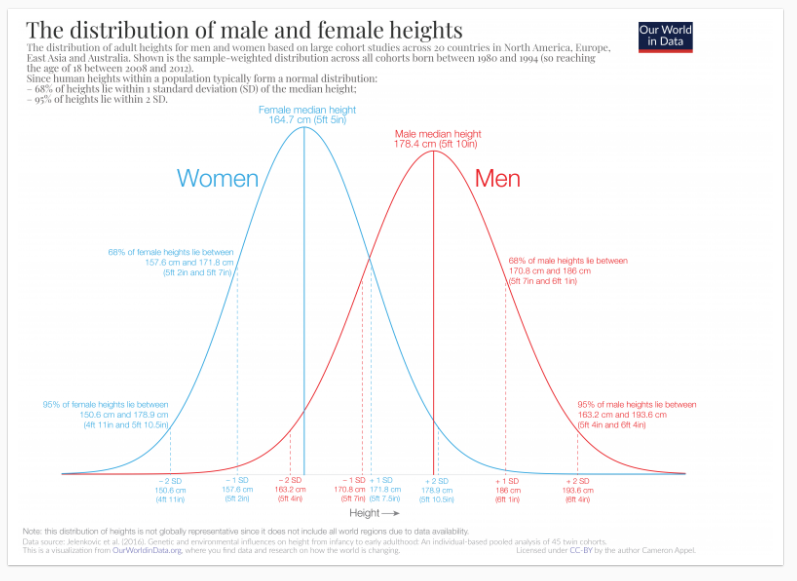
          • Height is approximately normal
          • This says that the mean, median and mode are about the same,
          • And that the data follows the bell curve.
          • 
          • 
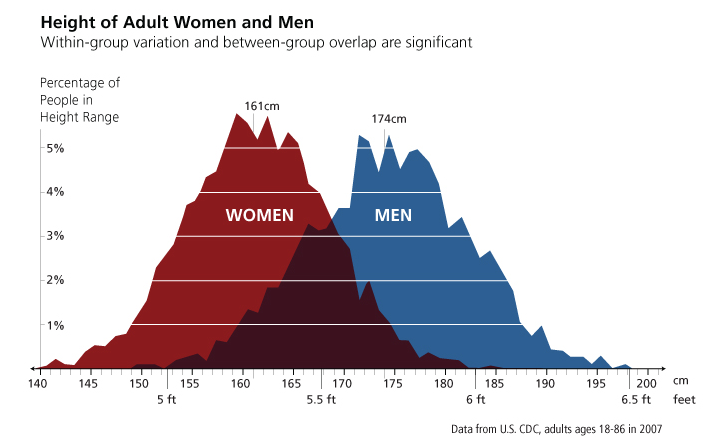
        • So we can be a little worried about the difference here.
        • Back to the sandbox
          • We can generate a normal distribution for men
            • mean = 172
            • Standard deviation = 10
            • =norm.inv(rand(), 172, 10)
            • Copy this down.
            • Name the range.
            • Compute mean and median on this.
            • Draw Histogram.
            • Copy this histogram
            • Compute the histogram for height.
            • What do you see?
      • We will skip the mode for now.
    • The median is a measurement of position as well.
      • Half the data is above th median
      • Half is below.
      • We can look at the data that is at the 25^th position.
      • This is called the quartile.
      • There are many ways to compute the quartile functions in stats.
      • There are in excel as well.
        • The function takes a range and a stat to compute.
          • 0 means min
          • 1 means 25%
          • 2 means 50% or median
          • 3 means 75%
          • 5 is max.
        • =quartile is deprecated or has been replaced
        • =quartile.inc, =quartile.exc
        • I don't care which of the later you use, but I tend to use .inc
      • Compute the quartiles for height.
      • I think we have a problem here.
      • Draw a box and whisker plot for each.
      • Discuss outliers and inner quartile distance.