How has the speed of processors changed?
- Several things have contributed to the birth of Data Science
- The increase in storage space has led to ability to collect and store larger and larger data sets.
- The increase in processor speed has led to the ability to process these datasets.
- A prediction know as Moore's Law has held true when describing increases in computer power.
- In 1965 Gordon Moore predicted that the speed of computers would roughly double every year and a half.
- This is oversimplified, but it has mostly held true.
- Let's do a couple of computations to see how Moore's Law worked.
- Simple speed computation:
- Assume I purchased a bicycle in 2000 and want to ride to Daytona Florida.
- I can ride the bike at 10 MPH
- It is about 1,000 miles to Daytona
- Start excel.
- Place the following data in cells
- A1: Year
- A2: Jan 2000
- B1: Speed (MPH)
- B2: 10
- C1: Hours to Daytona
-
- Adjust the headings so everything fits.
- Make column B wider by moving the cursor over the right border of the cell header and double clicking.
- Repeat this with column C
- Bold and center the headings.
-
- We want to put the distance to Daytona in the worksheet, that way we can change it if we move.
- Place the following
- Cell A19: Distance to Daytona
- Cell C19: 1000
- Cell A20: Days to Double
- We will use 1.5 years or
- Cell C20: =1.5*365
-

- By the way, we can view the computations by pressing ctrl-~
-

- You can also do this by the Formula tab,Formula Auditing workgroup, Show Formula toggle, but I can never remember this.
- ctrl-~ turns this back off too.
- Now compute the time to Daytona at 10 MPH in cell C2.
- This is just the distance (c19) divided by the speed (b2)
- =c19/b2
-

- Looking at this, it would take me 100 hours to ride my bike to Daytona Fl at 10MPH.
- But we want to assume Moore's Law is in effect for my bike, so
- In cell A3 put =A2+C$20 (what is this)
- Note the $, more on this later.
- In cell B3 put =B2*2 (what is this)
- In cell C3 put =C2/2 (What is this)
-

-
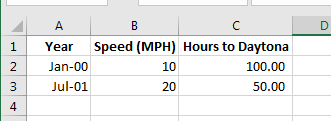
- Now we want to copy the entire computation through the year 2020.
- Highlight cells A3:C3
-
- Click-hold on the green box in the lower right hand corner of the green box
- Drag the corner down to cell C16 and release the button
-
- This will copy the formulas down and complete the computation.
-
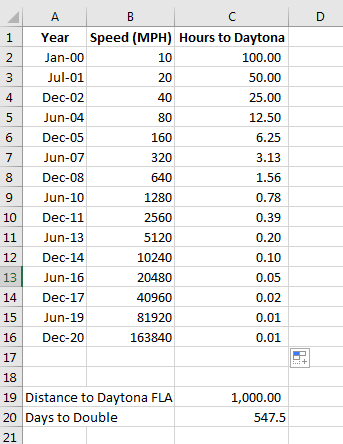
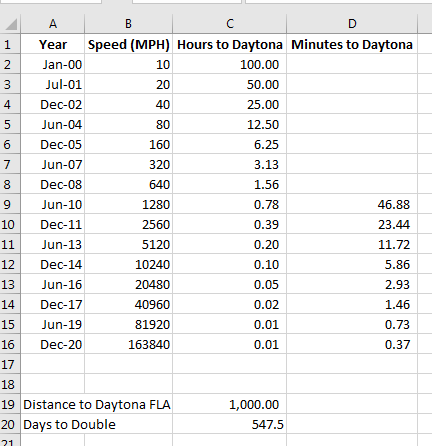
- I can't read fractional hours, so let's add a minute column
- In cell D1 put Minutes to Daytona
- In cell D9 put =C9*60
- Copy this down through cell D16
-
A more realistic example
- Password encryption
- In 1977, a VAX 780 could encrypt a password in .7111 seconds
- And a brute force attack on the password file would require 256 calls to encryption.
- It was sort of thought that this would be impossible to try all combinations.
- See this paper for more details.
- Start by getting a new worksheet
- At the bottom of the excel window click on the new worksheet button
-
- This will add a new worksheet tab at the bottom
-
- Click on this to change to the new worksheet.
- Add the following
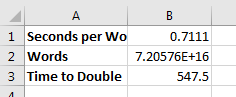
- In cell A1: Seconds per Word
- In cell B1: 0.7111
- In cell A2: Words
- In cell B2: 2^56
- In cell A3: Time to Double
- In cell B3: =365*1.5
- Format these nicely.
-
- Start to build a table
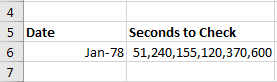
- In cell A5: Date
- In cell B5: Seconds to Check
- In cell A6: Jan 1978
- In cell B6: =B1*B2
- Format these nicely as well.
-
- In C5:F5 add labels for Minutes, Hours, Days and Years
- Compute the correct values in cells C6:F6 (divide by 60, 60 , 24, 365.25)
-

- Compute the next date and time required
- In cell A7: =A6+B$3 (note $)
- In cell B8: =B6/2
- Copy cells C6:F6 down.
-

-

- Copy Cells A7:F7 down through row 33
- My final worksheet:
-
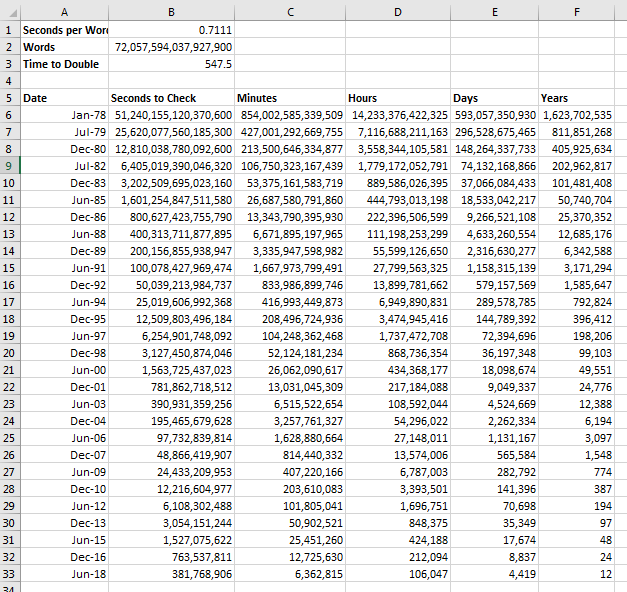
- A computation that would have taken 1.6 billion years in 1978 would now take 12 years.


















