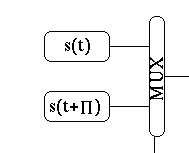Data Transmission

• Stallings' Key Points

  • All forms of information can be represented as electromagnetic signals.
  • All forms of information can be represented as either analog or digital.
  • Signals are composed of a number of frequencies.
  • The bandwidth of a signal characterizes the range of frequencies used to construct the signal.
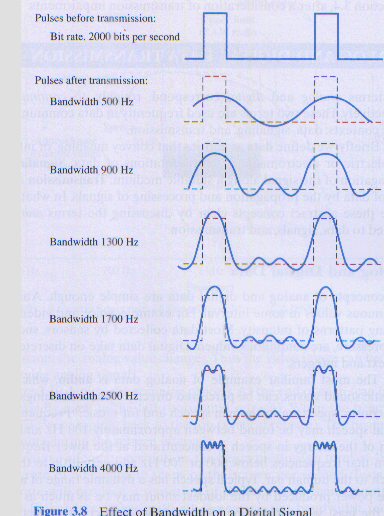
  • In general, the greater the bandwidth, the greater the information-carrying capacity.
  • Transmission impairment is a major issue in the design of communications facilities.
    • Attenuation
    • Attenuation distortion
    • Delay distortion
    • Noise

• Some Definitions

  • Guided Media carries the electromagnetic waves along a path (such as a cable)
  • Unguided Media allows the electromagnetic waves to travel as the will (wireless)
  • A Direct Link connects two devices without any intermediate devices (amplifiers, repeaters, ...)
  • A guided link is point to point if it directly connects two devices, and they are the only two devices on that media.
  • A link is multipoint if more than two devices are connected via the same media.
  • A Symplex connection allows one way communications. (FM radio)
  • A Half-Duplex connection allows two way transmission, but only one at a time.
  • A Full-Duplex connection allows simultaneous two way transmission.

• Time Domain Concepts

  • A signal is really a function of time s(t)
  • An analog signal varies smoothly WRT time.
    • lim_t->as(t) = s(a) for all a
  • An digital signal maintains a constant level for a time period, then (possibly) has an abrupt change to a new level.
    • But we will see this is not really true.
  • We will generate signals using a sine wave
    • A sine wave is characterized by
      • Amplitude [A] (in volts) or how high the sine wave goes.
      • Frequency [f] (in Hertz) or how frequently the sine wave repeats.
      • Phase [φ] (in radians)
      • s(t) = A sin(2*π*f*t+φ)
      • Period (T) is how long a single cycle takes, and this is 1/f.
      • Explore this with gnuplot.
      • The wavelength is the distance between two corresponding points on a wave.(λ).
        • If the signal is traveling at velocity v.
        • λ = vT
        • Or λf = v
        • Stallings points out that in air, λ=3x10⁸m/sec

• Frequency Domain Concepts

  • We can begin to shape the sine wave by adding additional frequencies
    • s₁(t) = sin(2πft)
    • s₂(t) = 1/3 sin(2π3ft)
    • s₃(t) = 1/5 sin(2π5ft)
    • plot
      • s₁(t)
      • s₁(t)+s₂(t)
      • s₁(t)+s₂(t)+s₃(t)
      • 4/π(s₁(t)+s₂(t)+s₃(t))
  • In this case, we are using frequencies f, 3f, and 5f
  • They are all integer multiples of a single frequency (f)
  • When this occurs, f is called the fundamental frequency
    • The period of the entire signal is the period of the fundamental frequency.
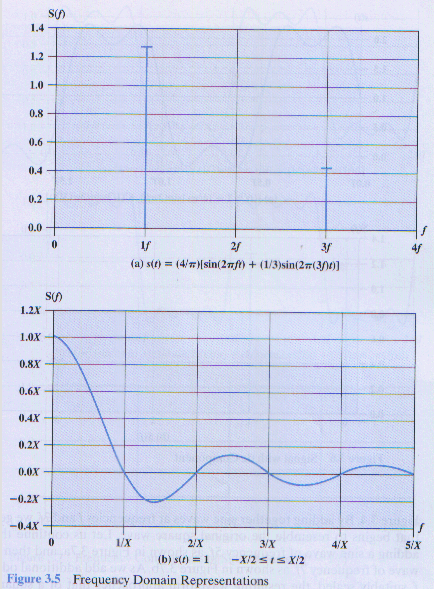
  • In the time domain, s(t) specifies the amplitude of the signal at time t.
  • In the frequency domain S(f) specifies the peak amplitude of the signal at frequency f.
  • Figure 3.5 a and b show this function for the function above and for a square pulse.
  • 
  • The spectrum of a signal is the range of frequencies it contains.
  • The absolute bandwidth of a signal is the width of the spectrum
  • The effective bandwidth of a signal is the width of the spectrum where most of the energy is located.
  • The effective bandwidth is also called the bandwidth
  • In 5.3a, the bandwidth is 3f-f or 2f
  • Finally we may want to move the signal up or down
    • We do this by adding a dc component

• Data Rate and Bandwidth

  • We can build a signal to match our data as closely as we wish
  • s(t) = A * 4/π * &Sigma_{k odd, k=1}^infinitysin(2πkft)/k
  • And encode bits by selecting either s(t) or s(t+π);
  • 
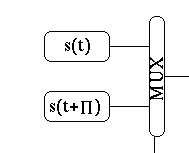
  • Notice we get 2 bits/cycle
  • The problem is, this requires infinite bandwidth.
  • And in the end, frequency k, only contributes 1/k energy.
  • So we limit this to the first few frequencies.
  • A few data rate computations:
    • Let s(t) = 4/π (sin(2*πft)+1/3sin(2*πft) + 1/5sin(2*π5ft))
    • Let f= 1MHx.
      • The Bandwidth is 5f-1f = 4f or 4MHz
      • 1 second/1x10⁶cycle x 1 cycle/2 bits = 1/2 μ second per bit
      • 1x10^{6 cycles/second x 2 bits/cycle = 2x106 or 2 Mbps}
    • Double the frequency, f = 2MHz.
      • The bandwidth become 4f or 8MHz.
      • The data rate becomes 2MHzx2bits/cycle = 4Mbps
    • Let s(t) = 4/π (sin(2*πft)+1/3sin(2*πft))
    • f = 2MHz.
      • The bandwidth becomes 3f-1f = 2f or 4MHz.
      • The data rate is still 2MHz x 2 bits/cycle or 4Mbps
  • The frequency tells us the data rate.
  • The bandwidth describes how much energy we need to use.
    • Greater bandwidth implies better signal
    • But also more power (more expensive)
  • So the higher the frequency, the more bandwidth is needed to send a clear signal.
  • Look at figure 3.8
  •