A Lower Bound on Comparison Based Sorting

• We have seen several $O(n \log_2 n)$ sorts, so should we look for better.
• But should we expect asymptotically better?
• The following assumes:
  • We are sorting a list of unique numbers.
    • This is not unreasonable.
    • And it just makes the following argument easier.
  • A sort derives all information using a comparison operator.
    • Given the first assumption == and != are out.
    • In some sense >, >=, <, and <= are all the same.
    • Each gives one piece of information.
• Sorting, in some real sense is finding the correct permutation of the input.
  • For n items, there are $n!$ possible permutations.
  • We need to model the decision to go from the input to the correct permutation.
• A decision tree lets us represent the work the sorting algorithm does
  • Each internal node represents a comparison.
  • 
  • Each leaf node represents one permutation of the input.
    • As stated above, there will be at least $n!$ of these.
  • 
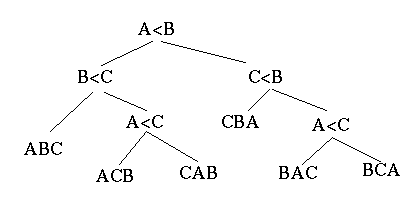
  • A path from the root to a leaf represents the comparisons that need to be made to "sort" the data.
• The level of a tree is the distance from the root.
  • In a binary tree at level h, there are at most $2^h$ nodes.
    • At level 0 there are $2^0$ = 1 node.
    • At level 1 there are $2^2$ = 2 nodes.
• Then a tree with $2^h$ leaves must have high h.
• So the best decision tree we can build with $n!$ leaves must satisfy $n! \le 2^h$
• or $h \ge \log_2 n!$
• A great Scotsman, James Sterling, provided a reasonably accurate approximation for $n!$, Sterling's approximation
  • $n! \approx e^{-n}n^n\sqrt{2\pi n}$
• So $h \ge \log_2{(e^{-n}n^n\sqrt{2\pi n})}$
• Remember $\log(ab) = \log a + \log b$
• So $h \ge \log_2{e^{-n}} + \log_2{n^n} + \log_2{\sqrt{2\pi n}}$
• $h \ge -n\log_2{e} + n\log_2{n} + \frac{1}{2}\log_2{2\pi n}$
• Which means $h \in \Omega (n \log_2 n)$