NP Complete and Reduciblity

• There is a special subset of the set NP
  • This is the set NP-COMPLETE
• A problem p, is in the set NP-COMPLETE if
  • $p \in NP$
  • Every problem $q \in $ NP-COMPLETE can be mapped to p in polynomial time.
• The last item is called a reduction, more on that soon.
• But the set NP-COMPLETE is essentially a set of problems that are all equally hard.
  • Or if I can solve one problem form this set in polynomial time, I can solve all of them in polynomial time.
• The idea of a reduction is that it is "easy" to turn one problem into another
  • Easy means it can be done in polynomial time.
  • The notation in CLRS is strange $P_1 \le_P P_2$ here $P_1 $ and $P_2$ are problems.
    • There exists an algorithm that maps all instances of $P_1$ to an instance of $P_2$ in polynomial time.
    • And by implication, after solving $P_2$ we can find the solution to $P_1$ in polynomial time.
    • This last part is not hard, remember, we are working with decision problems.
• By reducing one problem to another, we show that the new problem must be as hard as the original problem
  • Ie if $P_1 \le_P P_2$ and $P_1 \in P$, then $P_2 \in P$
  • Your author says that the hardness of $P_1$ is spread to $P_2$
• So the formal definition of NP-Complete is that $X \in $ NP-COMPLETE iff
  • $ X \in NP$
  • $ Y \le_P X $ for all $Y \in NP$
• For a while, apparently, they did not know if NP-COMPLETE was empty.
  • The problem is the second condition.
  • We need to reduce everything in NP to something.
• Circuit Satisfiablilty (CIRCUIT-SAT)
  • Given an single output arrangement of circuits, is there any input set that will produce a 1?
    • Consider F(a) = a and not a.
    • Consider F(a,b) = a or b.
  • Is this in NP?
    • Given a circuit and an input, can we check to see that the circuit evaluates to 1 in polynomial time?
    • Essentially we need to evaluate the value of each gate.
    • This is O(n) where n = the number of gates in the circuit.
  • Do we think we can find an answer quickly?
    • So far, the only way we know is to try all input possibilities.
    • For n inputs, there are $2^n$ possible inputs.
    • So the brute force algorithm is $O(2^n)$.
• The final part to show that CIRCUIT-SAT is NP-COMPLETE is to reduce all problems in NP to it.
  • This is really clever.
  • And we will just do a basic sketch of the proof.
  • (CLR says it is beyond the scope of that book).
• To map any NP problem to CIRCUIT-SAT
  • The input of the problem can be mapped to a binary string of length n, which will be the input to the circuit we will build.
  • IE we will build a circuit that will take the input to a decision problem and produce a 1 if the input is correct.
• Can we "emulate" a program with a circuit?
  • Clearly, this is just what a computer does.
  • A CPU is a circuit that takes an input and produces a state or output.
  • And this is constructed from a finite number of gates.
• We could picture execution of a single instruction
• 
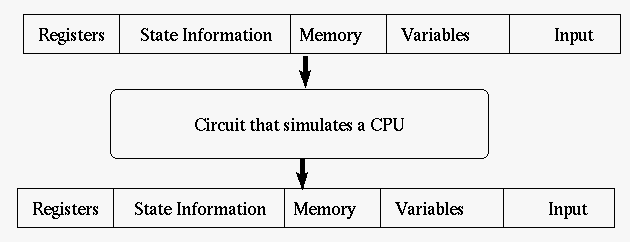
  • Note that everything is fixed except the variables and the input.
  • And that some place in the variables is a bit that stores if the input produces a 1 or a 0.
• Note that the CPU Simulation circuit is
  • A constant size.
  • Constructed of only and or or not gates.
  • Ie it is a circuit.
• So how does this help?
  • If a problem is in NP, then there exists a polynomial time algorithm that can verify if a solution is correct.
  • A polynomial time algorithm is just a polynomial number of machine instructions.
  • So we could build a circuit that simulates the entire set of instruction for the checker algorithm.
• If we can find a set of input that satisfies this circuit, we have the input that will solve the original problem.
• Since every problem in NP has a polynomial time algorithm to check it, we now have reduced every problem in NP to CIRCUIT-SAT.
• And CIRCUIT-SAT $\in$ NP-COMPLETE.