Further NP Complete Proofs
- Clean up a few definitions.
- A problem h is in NP-HARD if every problem in NP can be reduced to h in polynomial time.
- This can include problems that are not in NP.
-
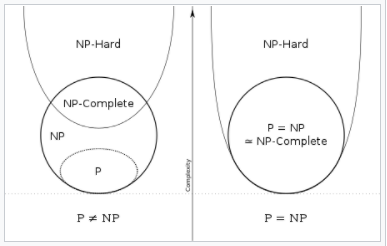 (Stolen from Wikipedia).
(Stolen from Wikipedia).
- A problem c is in co-NP is the set of problems who's compliment is in the class NP.
- We really don't need this.
- We have seen how CIRCUIT-SAT is NP-COMPLETE.
- It becomes much easier to show other problems are NP-COMPLETE now just by reducing CIRCUIT-SAT to them.
- A next logical step is SAT
- Given a boolean formula
- Composed of n variables $x_1, x_2, ... x_n$
- M boolean operations (AND, OR, NOT, ...) with two inputs.
- Parenthesis to change order.
is there a input such that the formula produces a true (or 1)?
- SAT $\in $ NP
- Clearly given an input, we can evaluate it in polynomial time.
- The proof that SAT is NP-COMPLETE is done by CIRCUIT_SAT $\lt_P$ SAT
- While not quite a straight forward as you might think, this is not too bad.
- The problem is keeping the construction of an equation from a circuit polynomial.
- When the gates can have more than two inputs.
- But it can be done.
- This continues
- Wikipedia has an article listing some problems.
 (Stolen from Wikipedia).
(Stolen from Wikipedia).
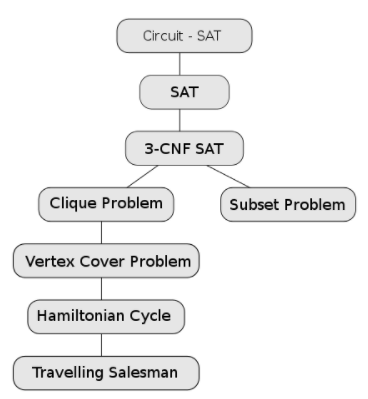 Stolen from Wikipedia again, but they took it from CLRS.
Stolen from Wikipedia again, but they took it from CLRS.