Asymptotic Notation

• Since we are talking about timing algorithms, it is safe to limit all functions to be non-negative.
• Since we are talking about timing algorithms, it is safe to limit all functions to be non-negative.
• To start things off, three definitions.
  • $O(g(n)) = \{f(n) : \exists ~ c > 0, n_0 > 0 \ni 0 \le f(n) \le cg(n) ~ \forall ~ n \ge n_0\}$
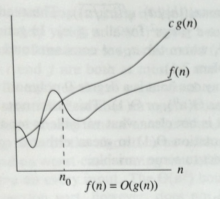  • (Figure from CLR)
  • $\Omega (g(n)) = \{f(n) : \exists ~ c > 0, n_0 > 0 \ni 0 \le cg(n) \le f(n) ~ \forall ~ n \ge n_0\}$
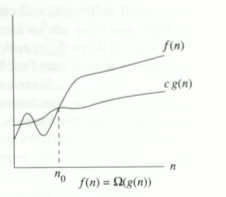  • (Figure from CLR)
  • $\Theta (g(n)) = \{f(n) : \exists ~ c_1 > 0, c_2 > 0 , n_0 > 0 \ni 0 \le c_1g(n) \le f(n) \le c_2g(n) ~ \forall ~ n \ge n_0\}$
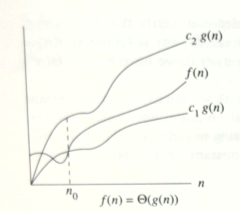  • (Figure from CLR)
  • $n_0, c, c_1$ and $c_2$ are all constants.
• Or
  • $O$ is bound from above, a function is no worse (larger) than this.
  • $\Omega$ is bound from below, a function is no better (smaller) than this.
  • $\Theta$ is bound from above and below, these functions are asymptotically the same.
• Note, these are sets of functions.
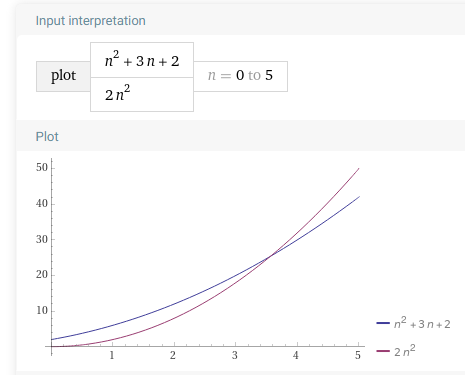
  • It is right to say that $n^2+3n+2 \in O(n^2) $
  • It is common to say that $n^2+3n+2 = O(n^2) $
  • It is common to say that $n^2+3n+2 $ is $ O(n^2) $
• But is $n^2+3n+2 \in O(n^2) $?
  • To show this, we would need to find $c>0, n_0 > 0$ such that $n^2 + 3n + 2 \le cn^2$ when $n > n_0$.
  • $$ \begin{eqnarray} n^2 + 3n + 2 \le cn^2 \\ 1 + \frac{3n+2}{n^2} \le c \\ \end{eqnarray}$$
  • Looking at $\frac{3n+2}{n^2}$, it is clear that for $n > 3$, this term is less than 1, so select $c = 2$ and $n_0 = 4$.
  • 
  • By the way, this is not really an exercise you do.
• But what are we doing here.
  • Remember we are looking at primitive operations.
  • In general, we mean operations that can be performed by a CPU in a single cycle
  • But remember from architecture, different CPUs have different instruction sets.
  • Consider
    • This program: code.cpp
    • In mips.s mips assembly code
    • $m(n) = 25n+10$
    • In intel.s mips assembly code
    • $i(n) = 11n + 6$
  • Are these two really different?
    • Again in architecture you considered things like CPI, Instructions, Clock Cycle length.
    • Here we just say $m(n) \in O(n^2) $ and $i(n) \in O(n^2)$
    • So the two are really equivalent.
  • in some sense we are saying
    • Ignore the startup costs
      • these are the constants (+10 and +6).
    • Ignore the difference in instruction count in the loop.
      • These are the coefficients (25 and 11)
    • Eventually for $n>10, i(n) \le 26n$ and $m(n) \le 26n$
• Just a final note.
  • O(n) is an upper bound.
  • $n^2 \in O(n^2)$,
  • $n^2 \in O(n^3)$,
  • $n^2 \in O(n^1000)$,
  • The first is a tight upper bound.
  • We like tight upper bounds.
  • And lower bounds, and total bounds too.