Approximation Algorithms

• Any attempt to solve problems in NPC, or the associated optimization problems must be done in a brute force manner.
  • We can obtain the solution.
  • But only for sufficiently small input.
• Consider the TSP problem
  • Given a complete graph G(V,E), and a weight function W(E)
  • Find the shortest possible path to visit each city once and return to the starting point.

  • TSP(G,s)
    
     l ← ∞
     for each permutation P of V starting at vertex s do
        append s to P
        w = COMPUTE_COST(P)
        if w < l  then
          l ← w
          R ← P
     return R
    
    	 

  • Line 2 is possible
    • but it is (n-1)!
    • We skipped this section, but it is really interesting
    • You SHOULD look it over, 4.3
    • But it is somewhat complex.
  • Line 4 is just O(|V|+lookup cost)
  • Standard Questions
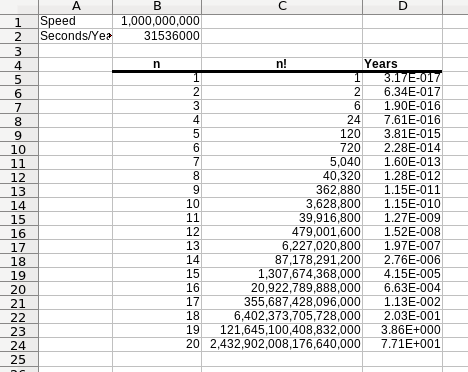
  • Notice how quickly this becomes bad.
  • 
• If we are willing to sacrifice complete accuracy can we do (predictably) better?
• An approximation algorithm attempts to find an approximate solution to a hard problem (or perhaps not so hard)
• A note on computing error
  • Let f(x) be the function we wish to maximize/minimize
  • Let s^* be the ideal solution.
  • Let s_a be the approximate solution.
  • The relative error will be

    	 f(sa)-f(s*)
    e(sa) = ------------
    	   f(s*)
    	 

  • Frequently this is simplified to
    • r(s_a) = f(s_a)/f(s^*) for minimization problems
    • and r(s_a) = f(s^*)/f(s_a) for maximization problems
    • This means that
      • The ratio will be bigger than one.
      • And that the larger it is, the worse the solution.
      • Or the smaller the better!
  • A polynomial algorithm is said to be a c-approximation algorithm where c ≥ 1 if r(s_a) ≤ c for all instances of s_a produced by the algorithm.
• TSP Approximations
  • Nearest Neighbor Algorithm
    • This is a greedy algorithm, we will discuss these, perhaps briefly later.
    • General Idea: at each step, pick the locally best solution.

    • NEAREST_NEIGHBOR_TSP(G=(V,E))
      
       Select a starting city at random
       while not all u ∈ V have been visited do
          select the least cost path out of the last vertex which does not lead to a selected city.
       add in the path from the last city to the start.
      
      	     

    • Consider this graph
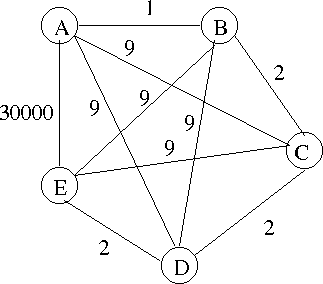
    • I believe f(s^*) = 23
    • Standard questions.
    • Select either A or E as a starting point.
    • Can I make this as bad as I wish?
  • Multifragment-heuristic algorithm

    • MHA_TSP(G=(V,E))
      
       Add all edges to the min-heap H
       count ← 0
       T ← {}, P ← {}
       while count < |V| do
           e=(u,v) ← H.Extract_Min()
           if u ∉ P or v ∉ P do
               add e to T
               if u ∉ P then
                   add u to P
               if v ∉ P then
                   add p to P
       Find u ∈ P and v∈ P such that each vertex appears in T only once
       Add (u,v) to T
       return T
      
      	     

    • Same questions for the same graph.
  • he presents a proof that NO polynomial time approximation algorithm to the generic TSP problem exists (if P ≠ NP).
  • But if we restrict the graphs somewhat
    • The triangle inequality holds
      • For a ∈ V, b ∈ V and c ∈ V, W((a,c) ≤ W((a,b)) + W((b,c))
      • This is natural for distances, and many other things as well.
    • symmetry holds
      • For a ∈ V and b ∈ V, W((a,b)) = W((b,a))
      • This is also a reasonable restriction for physical problems.
  • Twice Around the tree Algorithm
    • This is based on the minimal spanning tree algorithms.
    • These (Prim's and Kruskal's) are polynomial.
    • And we will look at them later.
    • But starting from a node, they find the lowest cost path to every other node
    • Which turns out to be a tree.
    • 
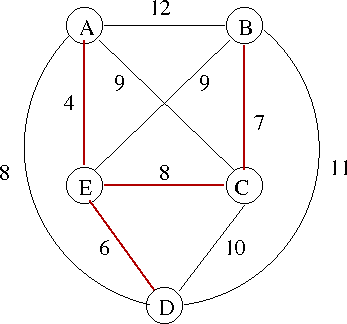
    • The conditions hold,
    • And the MST is marked in red.
    • Algorithm
      MST_TSP(G=(V,E))
      1. M ← MST(G)
      2. Perform A DFS traversal of the tree M
      3. At each node n, add n to T
      4. Scan T for any vertexes that are repeated (except for the first) and remove that edge.
    • 
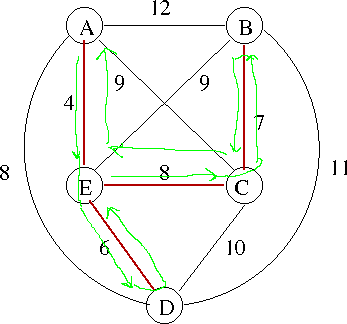
    • T = {A,E,D,E,C,B,C,E,A} after step 2.
    • T = {A,E,D,E,C,B,C,E,A} = {A,E,D,C,A} after step 3.
    • So we replaced {D,E,C} with {D,C}, is this legal?
    • So we replaced {B,C,E,A} with {B,A}, is this legal?
    • 
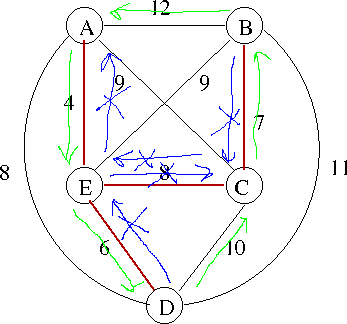
    • Are these substitutions legal? Why?
  • The MST_TSP is a 2-approximation.
    • Let s_a be the solution produced by MST_TSP
    • Let T^* be the minimal spanning tree for G.
    • Let s^* be the optimal solution.
    • Removing any edge from s^* yields a spanning tree, T.
    • W(s^*) ≥ W(T) ≥ W(T^*)
    • so 2*W(s^*) ≥ 2*W(T^*)
    • But because of the triangle inequality 2*W(T^*) ≥ W(s_a)
    • So 2*W(s^*) ≥ W(s_a)
  • He presents several other approximation algorithms.