Heap Sort

• A heap is a data structure
  • It is a binary tree
  • With the following properties
    • All levels except the last are full, and the last is filled from the left to the right.
      • This is know as essentially complete
      • There are at most 2^l nodes at level l.

        To Prove: There are at most 2l nodes at level l in a binary tree.
        By induction:
        Prove true for the base case
          At level 0 there are at most 20 = 1
        Strong Induction: Assume true for k
          At level k there are at most 2k nodes.
        Prove for k+1
          To show:  At level k+ there are at most 2k+1 nodes.
          By the inductive step, there are at most 2k nodes at level k.
          Since it is a binary tree, each node at level k may have two children, so
          there are at most 2*2k nodes at level k+1.  
          Since 2*2k = 2k+1 the proof is complete.
        		    

      • it is also easy to show that there are a maximum 2^h+1-1 nodes in a complete binary tree.
      • And that a binary tree is at least ⌊lg(|V|)⌋ high
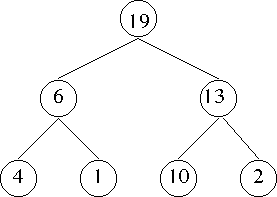
    • The second property is the heap property
      • The key for any node is greater than the key for all descendant nodes.
      • Leaf nodes automatically meet this property.
      • And it is recursive, so sub-heaps are also heaps.
      • This is a maximum heap, the maximum is at the top.
      • We can also require a minimum heap where the minimum is at the top.
    • 
  • Heap operations
    • let n = |V|
    • Insert an item into the heap
      • This should be O(lg(n))
      • Because we need to maintain the heap.
    • Delete the top item from the heap
      • This should be O(lg(n))
      • Because we need to maintain the heap.
    • Normal observers such as height, isEmpty, size..
      • Should all be maintained as aux data.
      • And should all be O(1) time.
  • Implementation
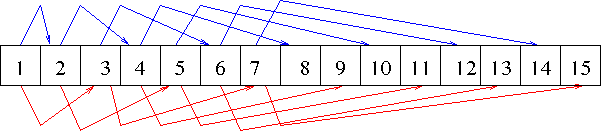
    • Observe the following properties of an array
      • Place the root at A[1], I know this is a FORTRAN thing, but ...
        • But it makes the computation easier
        • And we can always subtract 1 from all of the computations below.
      • So now consider the relationships between index and children:
        • A left child could be at position 2, (or 1*2)
        • A right child could be at position 3 (or 1*2+1)
      • For the node at position 2
        • The left child is at 2*2 or 4
        • The right child is 2*2+1 or 5
      • For the node at position 3
        • The left child is at 3*2 or 6
        • The right child is 3*2+1 or 7
      • For node 7, the parent is ⌊7/2⌋ = 3
      • For node 6, the parent is ⌊7/2⌋ = 3
      • 

      • PARENT(i) 
        
         return i/2
        
        
        Right(i) 
        
         return i*2+1
        
        
        PARENT(i) 
        
         return i*2
        
        		   

      • 
    • An important routine is HEAPIFY
      • Takes an array A and a position i.
      • Assumes that the sub-heaps are heaps
      • But the item at position i might not be.

      • HEAPIFY(A,i)
        
         l ← LEFT(i)
         r ← RIGHT(i)
         if l ≤ HEAP_SIZE(A) and A[l] > A[i] then
             largest ← l
         else
             largest ← i
         if r ≤ HEAP_SIZE(A)  and A[r] > A[largest] then
             largest ← r
          if  i ≠ largest then
             SWAP(A[i],A[largest])
             HEAPIFY(A,largest)
        
        			

      • What does this do?
      • Are we sure it is right?
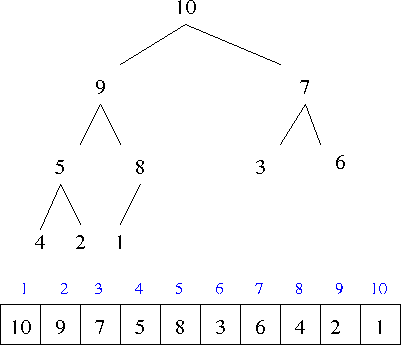
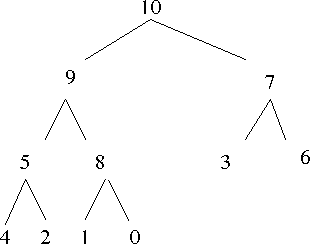
      • Consider HEAPIFY(A,1)
        • 
        • Call 1 will swap 0 and 10 and call HEAPIFY(A,2)
        • Call 2 will swap 0 and 9 and call HEAPIFY(A,5)
        • Call 3 will swap 0 and 8 and call HEAPIFY(A,11)
        • Call 4 will exit due to HEAP_SIZE()
        • 
      • What is the performance
    • BUILD_HEAP will take an array and turn it into a heap.

      • BUILD_HEAP(A)
        
         HEAP_SIZE(A) ← length[A]   // perhaps an abuse of notation.
         for i ← ⌊length[A]/2⌋ down to 1 do
             HEAPIFY(A,i)
        
        			

• This can all lead to HEAP_SORT

  • HEAPSORT(A)
    
     BUILD_HEAP(A)
     for i ← length[A] down to 2 do
         SWAP(A[1],A[i])
         HEAP_SIZE(A) ← HEAP_SIZE(A)-1   // perhaps an abuse of notation.
         HEAPIFY(A)
     return