CIRCUIT_SAT is in NPC

• This is again the 10,000 ft view.
• Given a boolean combinational circuit composed of AND, OR, and NOT gates, is it satisfiable?
• The problem assumes
  • And, not and or gates
  • no loops (combinational circuits only)
  • A single wire may be split to several gates.
  • Inputs and outputs are clearly defined.
• CIRCUIT_SAT is in NP
  • The verification algorithm simply checks the circuit and produces a true if the value is one for a given input.
• CIRCUIT_SAT is in NPC
  • A running program on a computer consists of the input, the program and the current state of the computation
    • Stack, registers, PC, memory ...
  • This state can be represented at any point in the computation.
  • This is called a configuration
  • The hardware (aside from memory) can be created as a circuit M
  • For any Problem L in NP, we have V_L which verifies L.
  • V_L ∈ P
  • We need to find R_L which reduces L to CIRCUIT_SAT in polynomial time.
  • Let T(n) be the worst case running time of V_L on an n bit input.
  • Since V_L ∈ P, there exists a k such that T(n) ∈ O(n^k)
  • Since V_L verifies L, there is a location in the configuration of the execution of V_L which will indicate if a given certificate is correct or not (answer).
  • 
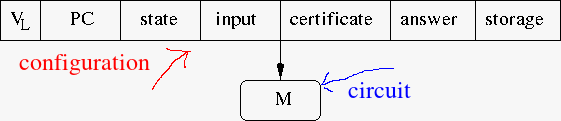
  • So each output of a circuit goes to a configuration and each configuration goes to a machine.
  • Each time the PC will change
  • 
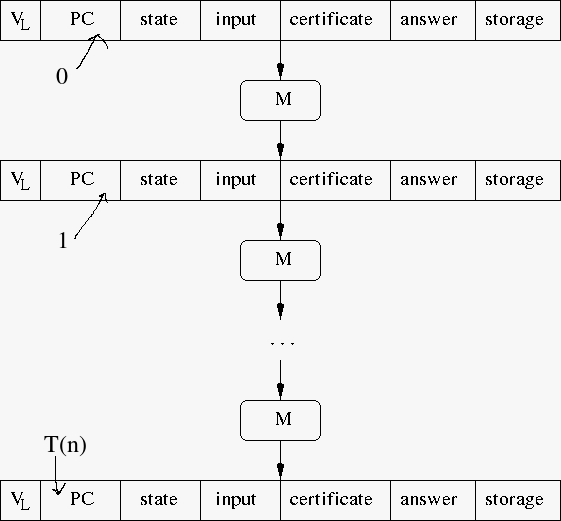
  • Construction of this circuit will require polynomial time (T(n))