More Dynamic Programming

• Change Making
  • You need to make change,
  • You have coins of values d₁, c₂ ....
  • You wish to make the change with the minimum coins.
  • Let F(n) be the minimum number of coins which will add up to n
    • F(0) = 1
    • F(n) = min{F(n-d_j}+1 over all j wuch that n ≤ d_j
    • Let's try with d={1,3,4} making change for 6

      n   :  0  1 2 3 4 5 6
      f(n):  0
      
       For F(1) we look over the set {1}, F(1-1)+1 = 0 + 1 = 1, which is the min
       (We can make change for 1 with 1 value 1 coin)
      
      n   :  0  1 2 3 4 5 6
      f(n):  0  1
       
        For F(2), we look over the set {1}, F(2-1)+1 = 1 + 1 =  2, which is the min
        We can make change for 2 with 2 value one coins
      
      n   :  0  1 2 3 4 5 6
      f(n):  0  1 2
      
        For F(3), we look over the set {1,3}, F(3-1)+1 = 2+1 = 3
                                              F(3-3)+1 = 0+1 = 1, the min
      n   :  0  1 2 3 4 5 6
      f(n):  0  1 2 1
      
        For F(3), we look over the set {1,3,4}, F(4-1)+1 = 1+1 = 2
                                                F(4-3)+1 = 1+1 = 2  
      			Notice, both represent one of each coin
      			                  F(4-4)+1 = 0+1 = 1 
      
      n   :  0  1 2 3 4 5 6
      f(n):  0  1 2 1 1
          
        For F(5), we look over the set {1,3,4}, F(5-1)+1 = 1+1 = 2
                                                F(5-3)+1 = 2+1 = 3  
      			                  F(5-4)+1 = 1+1 = 2 
      
      n   :  0  1 2 3 4 5 6
      f(n):  0  1 2 1 1 2
      
        For F(6), we look over the set {1,3,4}, F(6-1)+1 = 2+1 = 3
                                                F(6-3)+1 = 1+1 = 2  
      			                  F(6-4)+1 = 2+1 = 3 
      	    

    • He provides the following algorithm:

    • CHANGE_MAKING(D[1..m],n)
      
       F[0] ← 0
       for i ← 1 to n do
          temp ← ∞
          j ← 1
          while j ≤ m and  i ≥ D[j] do
               tmp ← min(F[i-D[j],tmp)
               j ← j + 1 
          F[i] ← tmp + 1
       return F[n]
      
      	    

    • Time and space complexity?
    • Does it work?
    • Can we do better?
• Assembly line scheduling
  • From CLRS
  • Assume we have two assembly lines which produce the same item.
  • The lines both have the same number of stations
  • But some of the stations may take different times, even at the same stage.
  • And there is a cost for transfering an item between stations..
    • e_i is the cost to enter line i
    • x_i is the cost to exit line i
    • s_i,k is the cost to pass through station k of line i
    • t_i,k is the cost to transfer from line i to the other line after stage k.
  • 
  • Consider the following example:
  • F[i,j] represents the lowest cost to exit line i station j
  • F[0,j] = e_j
  • F[i,j] = min(F[i,j-1],F[-i,j-1]+t_-i,j-1]) + s_i,j
  • The minimum of the price to go through previous station or to come from the other line.

      
       The first two are automatic
    
         0   1   2   3   4   5  6  7
    F 1  2   9
      2  4  12
    
      
      
      For 1,2 The price is either 9+9 or 12+2+9, 18
      For 2,2 The price is either 12+5 or 9+2+5 16
       
         0   1   2   3   4   5  6  7
    F 1  2   9  18
      2  4  12  16
    
      
    
      For 1,3 The price is either 18+3 or 16+1+3, 20 
      For 2,3 The price is either 16+6 or 18+3+6, 22
       
         0   1   2   3   4   5  6  7
    F 1  2   9  18  20
      2  4  12  16  22
    
      
    
    

  • Performance?
  • I believe we could do better.
    • Consider the following transformation
    • Transform all stations into verticies.
    • Transform all edge costs by adding the cost of the preceeding station.
    • Add a start and an end node
    • 
    • Now run ANY single source shortest path algorithm.
    • Like the generic one for DAGS

    • 
      INITIALIZE_SINGLE_SOURCE(G={V,E},s)
      
       foreach v ∈V do
           d[v] ← ∞
           π[v] ← NIL
       d[s] ← 0
      
      
      RELAX(u,v,w) 
      // w is a weight function
      
       if d[v] > d[u]+w(u,v) then
           d[v] ← d[u] + w(u,v)
           π[v] ← u;
      
      
      DAG_SHORTEST_PATH(G,w,s)
      
       TOPOLOGICAL_SORT(G)  (O(|V|+|E|))
       INITIALIZE_SINGLE_SOURCE(G,s) 
       for each u ∈V in topological order do
            
       for each  v ∈ ADJ(u) do
                 RELAX(u,v,w)
      
      
            
            
      
      Assume source = a, destination = f
      
            
      
      start at a,   b is adjacient to a, so call realax on (a,b) , new cost 5
                    c is adjacient to a, so call realax on (a,c) , new cost 3
      
            
      
      Go to b,    c is adjacent to b so call relax on (b,c), but this is no change
                  d is adjacent to b so call relax on (b,d), new cost 11
      
            
      
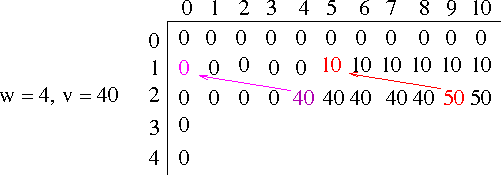      Go to c,    d is adjacent to c so call relax on (c,d), new cost 10
                  e is adjacent to c so call relax on (c,e), new cost 7
      	    f is adjacent to c so call relax on (c,f), new cost 4
      
            
      
            ...
            

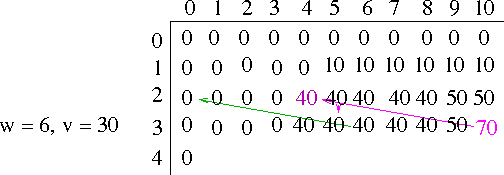    • Does it work?
    • What is the cost?