Empirical Analysis of Algorithms

• This is section 2.6.
• I have moved it due to my programming assignment.
• We will study how to analyze an algorithm's performance theoretically
• But sometimes this is very difficult.
• It is especially hard to determine average case analysis.
• Our author proposes a general plan for testing efficiency
  • Understand the experiment's purpose
  • Decide on an efficiency metric to be measured
    • Wall clock time.
    • Number of instructions executed.
    • Combination of the two (Xflops/second, x = mega, giga, tera)
  • Decide on characteristics of input.
  • Implement algorithms
  • Generate sample inputs
  • Run algorithms on input, record results
  • Analyze the data obtained.
• This type of testing is used extensively in the supercomputing world, see the top 500 list
• Several things to note:
  • We are testing implementation of algorithms, so there is another lay of potential error inherent in this experiment.
  • We need to be absolutely sure that our implementation has produced accurate results, so testing the final output of the algorithm implementation is essential.
• Measuring performance
  • We have discussed wall clock time.
    • We are measuring total time, so the system load will have an effect on this.
    • A quiet system is best
    • A single user system, with most things (like the window system, the web server, file servers, ...) turned off is absolutely best.
    • An average of several runs mitigates the impact of time.
    • Remember, runtime is relative to the system involved, so there is no "RIGHT" answer here.
    • If the process does not take sufficient time to be measured, run it a number of times on the same data.
    • In any case, clocks are problematic
      • Time is sometimes reported in "ticks", not in a normal unit.
      • Most clocks are not highly accurate.
  • As a second measurement, we could count operations.
    • For BRUTE-GCD algorithm we could insert a counter inside the loop.
    • Or we could maintain two counters, m%g and n%g should probably count as two operations, while g ← g-1 should count as one.
    • It is reasonable to employ a global variable here.
      • But make sure that you reset it each time in your driver routine.
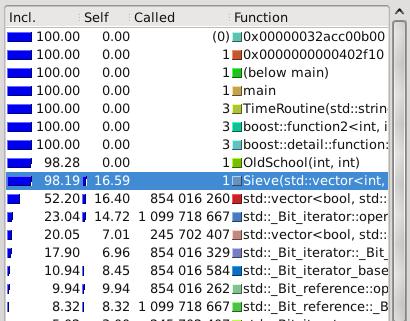
  • Finally you could employ an analysis tool such as Valgrind
    • This will give you performance information, (and memory leaks and ...)
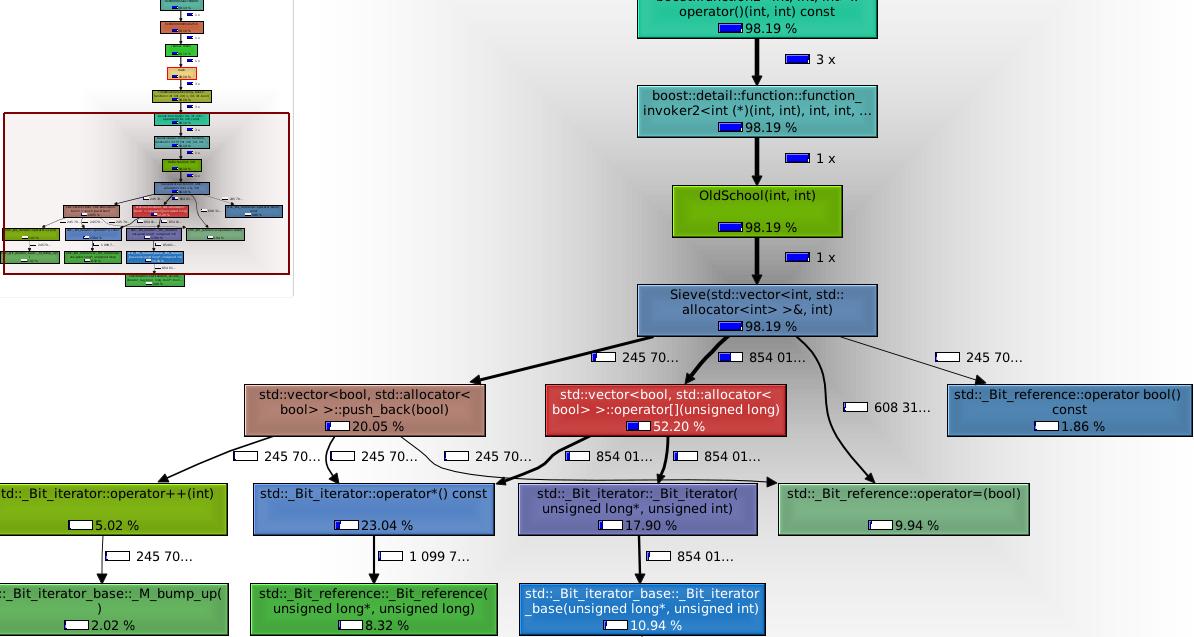
    • You can produce a call graph, based on time spent routines.
    • You can view the call tree.
    • This provides real insight into where the program is burning time.
    • 
    • 
• In order to estimate asymptotic performance, you need to run test cases with various sizes of input.
  • For some problems there are well established data sets (again, top500)
  • Others you must create your own.
  • The author suggests two methods for selecting input sizes.
    • Regular sizes within a range
      • This probably makes analysis easier.
      • But could lead to an error if your sizes are somehow "magical".
      • (Some algorithms might involve a log₂ structure, so a size of 2ⁿ is optimal, while 2ⁿ+1 might have dramatically different performance.)
    • Random samples within a range.
  • I am asking for the first, with random data used for the different test cases.
• Random Samples
  • Linear Congruential Method

  • RANDOM()
    
     tmp ← seed
     seed ← (a*seed+c) % m
     return tmp
    
    	

  • The values of a, c and m are very important.
    • c and m should be relatively prime
    • .01m ≤ a ≤ .99m
    • a%8 = 5
  • There are many sources of discussion on these choices.
  • This will produce a string of "pseudo-random" numbers which will repeat.
  • Compare this to the algorithm for the Mersenne Twister
    • Both in space and time complexity.
• When you run your programs, build an automatic way to collect and present the data.
  • I will frequently use a vector, to store times and information about the run (size, ...)
  • I would probably store this in an XML file these days, including other meta data.
  • I load this data into a spreadsheet and use the tools provided.
• Be careful of things like
  • log(n) vs time graphs (they will be distorted)
  • You collect sufficiently diverse data to see the results.
  • Automate your data collection and analysis.
    • Metadata collection and retention.
      • Version of the software
      • Input parameters
      • machine/environment/...
      • Compilation options
    • Data storage and organization (a reasonable naming convention)
    • If you are doing something long term, you will appreciate this.