- Do they terminate?
- Do they work?
- Performance?
- Why are they classified as brute force?
- Sequential Search
- He provides a minor update in line 1.
-
SEQUENTIAL_SEARCH2(A,k)
- A[n] ← k
- i ← 0
- while A[i] ≠ k do
- i ← i + 1
- if i < n
- return i
- else
- return -1
- The usual suspects
- Does this help?
- String Matching
- Given a text T and a pattern P, both constructed from an alphabet A, find position i of the first substring of T which matches P.
- string.find(pattern)
- Important: DNA and Genomic research
- This is a VERY active field of research.
-
BRUTE_FORCE_STRING_MATCH(T[0..n-1],P[0..m-1])
- for i ← 0 to n-m do
- j ← 0
- while j < m and P[j] = T[i+j] do
- j ← j + 1
- if j = m
- return i
- return -1
- Terminate?
- Work?
- How does it work.
- Performance?
- Computational Geometry is the study of problems which can be stated in terms of geometry.
- Important: robotics, GIS, circuit design, computer aided engineering, computer vision.
- We will look at a few problems in computational geometry now.
- And look at them again later!
- Closest Pair
- Given a collection of n points, find the pair which is closest.
- We need to be careful about closest, mathematicians have different measurements of distance.
- But for now, euclidean distance will do.
-
BRUTE_FORCE_CLOSEST_PAIR(P)
- d ← ∞
- for i ← 1 to n-1 do
- for j ← i+1 to n do
- d ← min(d, sqrt((xi-xj)2 + (yi-yj)2)
- return d
- Does it terminate?
- Does it work?
- Have we seen this pattern before?
- What is the performance?
- Can we make it more efficient? (remove sqrt?)
- Convex Hull
- Given a set of n points P in a plane, find the minimal convex polygon which encloses these points. (The points may be on the convex hull)
- A set of points in the plane is convex if for any two points p and q in the set, the entire line segment with the endpoints p and q belongs to the set.
- There are many applications for the convex hull.
- And there are many algorithms, some of which we will study later.
- Put pegs in a board ans snap a rubber band around those points, that is the convex hull.
- A convex hull of a set S of points is the smallest t convex set containing S.
- A side track
- The cross product of two 2D vectors
- u×v = uxvy - uyvx
- |u×v| = |u||v|sin(θ)
- sin(θ) = |u×v|/(|u||v|)
-
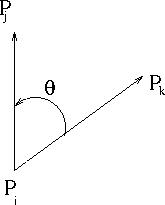
- The cross product of two 2D vectors
- By looking at the cross product, we can determine if a line (or point) is on the left or right of a given line.
- We can even tell if the points are colinier
-
BRUTE_FORCE_CONVEX_HULL(P)
- C ← {}
- for i ← 1 to n -1 do
- for j ← i+1 to n do
- state ← unknown;
- for k ← 0 to n do
- if i ≠ k and j ≠ k then
- Θ = mag(<Pi,Pj> × <Pi,Pk>)/ (mag(<Pi,Pj>)mag(<Pi,Pk>))
- if PiPjPk are colinear (Θ= 0)
- if Pk is between Pi and Pj
- continue
- else
- state ← NOT_IN
- elseif Θ < 0
- if state = unknown
- state ← left
- elseif state = right
- state ← NOT_IN
- else
- if state = unknown
- state ← right
- elseif state = left
- state ← NOT_IN
- if state ≠ NOT_IN
- C ← C ∪ <Pi,Pj>
- Does it terminate?
- Does it work?
- Performance?