Binary Search Trees

• A structure that supports maintaining data in an order to facilitate rapid searches.
• This tree must satisfy the binary search tree property
• Let x be a node in a binary search tree. If y is a node in the left subtree of x, then key[y] <= key[x]. If y is a node in the right subtree of x, then key[x] <= key[y]
• Build a binary search tree with keys 1, 4, 5, 10, 16, 17, 21 of various heights.
• By maintaining this property we can implement the binary search

• location Search(Tree T, element e)
  
   if T = NULL or e = key[T]
       return T
   if e < key[T]
       then return Search(T->left,e)
       else return Search(T->right,e)
  
      

• The performance of this algorithm is based on the height of the tree. O(h)
• The minimum can be located easily, just keep going left.

• location Minimum(T) 
  
   if T = NULL
      return T
   while T->left != NULL
      T = T->left;
   return T
  
      

• What would the algorithm for finding the maximum be?
• What is the performance of these algorithms?
• Finding the next node in the tree

• location Successor(tree T) 
  
   if T = NULL
      return T
   if T->right != NULL
      return Minimum(T->right)
   x = T
   y = T->parent
   while y!= NULL and x = y->right
      x = y
      y = y->parent
   return y
  
      

• The first part (lines 1-4) are clear, just the minimum right child if there is one.
• 
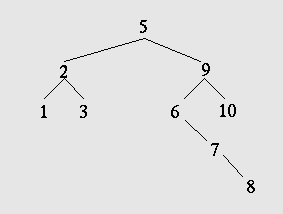
• Consider the successor to 2, 5 or 9
• The second part, we just move up the tree until we find a parent with a different right child.
• Consider 1, 3, 8, 10
• What is the performance of this algorithm?
• Inserting

• Insert(Tree T, element e) 
  
   y = NULL
   x = T.root()
   while x != NULL 
       y = x
       if key[e] < key[x->data]
           then x = x->left
           else x = x->right
   z = newnode
   z ->parent = y
   z -> left = NULL
   z -> right = NULL
   z -> data = e
   if y = NULL
       then T.root = z
       else if key[z->data] < key[y->data]
           then y->left = z
           else y->right = z
  
  

• Build a tree by inserting the following 5, 2, 9, 3, 1, 10, 6, 7, 8
• Deletion is a bit more tricky
  • We need to maintain the binary search tree property
  • If the node to be deleted is a leaf node, just delete it.
  • If a node is not a leaf node, but only has one child, replace it with it's child.
  • If a node has two children, then replace it with it's successor.

• Delete(Tree T, location z) 
  
   if z->left = NULL or z->right = NULL
       then y = z
       else y = Successor(z)
   if left[y] != NULL
      then x = left[y]
      else x = right[y]
   if x != NULL
      then x->parent = y->parent
   if y->parent = NULL
      then T.root = x
      else if y = y->parent->left
            then y->parent->left = x
            else y->parent->right = x
   if y != z
      then z->data = y ->data
   delete y
  
      

• In the previous diagram, delete 3
• Delete 5
• delete 6
• Not too bad, if we just didn't have the O(n) in the worst case.