Chapter 1, Introduction

• What is this class about?
  • We would like to examine how different algorithms and data structures behave. Describe their performance characteristics.
  • We are especially interested in what happens as the amount of data becomes large
  • What do we mean by large?
    • For the most part, problems you have solved in the past have involved small amounts of data.
    • A few to a few hundred data items.
    • In the real world, problems can become very large
      • Process all of the customers in a database
      • All of the citizens of a city/state/country
      • The text for a novel.
  • Is there anything we can do to mitigate the impact of the hardware on our study?
    • We would like a little more permanence that just: How fast does it run today?
    • You probably have seen something about this (O(n)) computations.
    • But we will work on this much more as the semester goes along.
  • A first Example: Given a list of n items, find the k^th smallest.
    • We must assume the items are not ordered.
    • Algorithm 1:

      FindItemK(A, n, k)
      
       sort(A,0,n-1)
       return A[k-1]
      
      	      

    • This assumes that the sort sorts items 0-n and places the smallest item at position 0.
    • In some sense this relates finding the k^th smallest item to sorting.
    • And the performance of the algorithm depends on the performance of sorting.
    • Let us experiment a bit.
      • We need to know about random numbers, srand, rand
      • We need to know about times
        • This is a system call that returns information about process time
        • It is returned in a time structure

          struct tms {
              clock_t tms_utime;  /* user time */
              clock_t tms_stime;  /* system time */
              clock_t tms_cutime; /* user time of children */
              clock_t tms_cstime; /* system time of children */
          };
          			

        • We need to include <sys/times.h>
        • Each call will return time used so far in each area

        • times(&start);
          perform task
          times(&end);
          

      • The code
      • We should probably investigate two things:
        • What happens when n changes?
        • What happens when k changes?
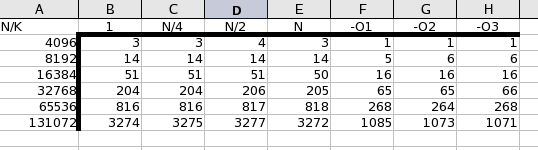
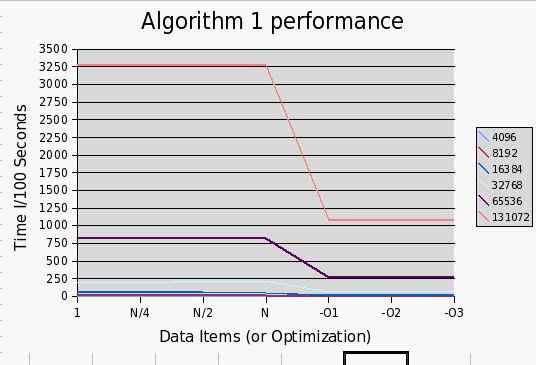
        • I ran the program on cslab177
        • 
        • 
    • Algorithm 2:

      FindItemK(A, n, k) 
      
       sort(A,0,k-1);
       for i<- k to n-1 do
          if (A[k-1] > A[i] do
              place(ary, k, ary[i])
       return A[k-1]
      
      

    • place is a routine that will insert an item into an an array at it's proper position.

      place(A, n, item)
      
       position <- n-1
       while position > 0 and A[position-1] > item do
          A[position] <-  A[position-1]
       A[position] <- item
      
      

  • Now we don't sort the entire list, so there is perhaps some work we don't do.
  • Test Conditions were the same
  • 
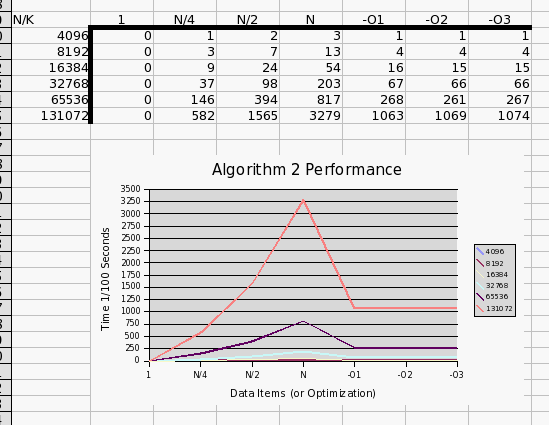
  • Notice for Algorithm 1, the results depended entirely on N
  • In Algorithm 2, they also depended on K.
  • How would we describe the behavior of these algorithms?
  • Are they good enough?
  • Can we do better?
  • Can we predict the time required for a given size N and K?