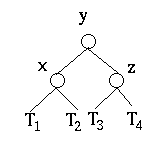Check on case 1 and 3

• Assume we have a tree such that key[x] < key[y]< key[z];
• This makes it case 1, but case 3 will work the same way.
• 
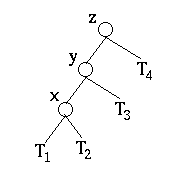
• The tree was ok before we added the new node.
• WLOG assume that the new node was added to T₁
  • It had to be T₁ or T2 because x is the ancestor of the node that was added.
  • It could be either
• We know that the trees at x and y are ok so.
  • let h(t) be the height of a tree t.
  • h(T₁) = h(T₂)+1, otherwise the tree didn't get any deeper, so there is no need to adjust the tree.
  • h(T₁) = h(T₃), since the tree at y is balanced, and T₁ just got one node higher
  • Again, if this were not the case, the tree would not be out of balance at z.
  • h(T₃) = h(T₄)+1, z was balanced and T₃ and T₄ did not change.
  • h(y) = h(T₄) + 2, since z is no longer balanced.
• After the rotation:
  • 
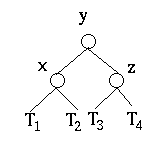
  • h(T₄) increased by 1.
  • h(T₃) remained the same.
  • h(T₂) decreased by 1.
  • h(T₁) decreased by 1.
  • h(T₃) = h(T₄)
  • h(T₃) = h(T₁)+1
  • h(T₁) = h(T₂)+1
  • So the AVL property is preserved.
• Note, h(y) is now the same as h(z_old)