Circuit Satisfiability

• A circuit is satisfiable if for a given input, the result is 1.
• This is satisfiable (x=1, y=1)
• 
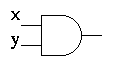
• This is not satisfiable
• 
• If you can show that a circuit is not satisfiable, you can eliminate it from your architecture and replace it with a 0.
• Given a boolean combinational circuit composed of AND, OR and NOT gates, determine if the circuit is satisfiable. (CIRCUIT-SAT)
• One approch is if there are n inputs, try all 2ⁿ possibilities
• This is defniately not a polynomial time algorithm.
• But given a set of inputs, we can check to see if they are correct in linear time.
• So this problem is in NP
• This is 1/2 of the proof to show that it is NP-Complete
• The second half (showing that every problem in NP-Complete can be reduced to it) goes as follows
  • A program consists of a memory store of the state (pc, registers, memory, ...)
  • Let M be a circuit implementing a computer.
  • Let A be the verification algorithm for any problem in NP
  • Let C be the certificate
  • A runs in polynomial time, and produces an 1 if C is correct, or a 0 if the cirtificate is incorrect.
  • Thus there are a series of k steps that M must perform using A to compute if C is correct.
  • Build a circuit to do this. (This is the reduction)
  • 
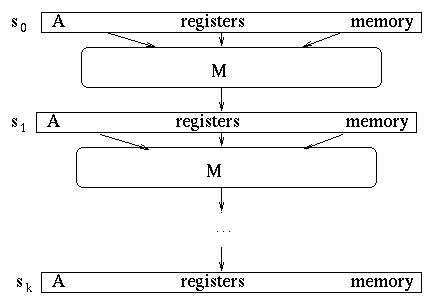
  • This circuit can be constructed in polynomial time
  • If this circuit is satisfiable, then the memory where C is stored will contain the answer to the problem we started with
  • Thus this is a polynomial time reduction of the problem to CIRCUIT-SAT
  • And thus CIRCUIT-SAT is in NP-Complete
  • This circuit can be constructed in polynomial time
  • If this circuit is satisfiable, then the memory where C is stored will contain the answer to the problem we started with
  • Thus this is a polynomial time reduction of the problem to CIRCUIT-SAT
  • And thus CIRCUIT-SAT is in NP-Complete