A lower bound on comparison baised sorting

• with n elements, there are n! possible arrangements.
• Any comparison can consider at most two elements at a time.
• We can represent a sort as a decison tree.
  • Each internal node represents a comparison between two elements.
  • Each leaf represents an ordering
  • A sort must start at the root and reach a leaf.
  • Consider sorting three elements.
  • 
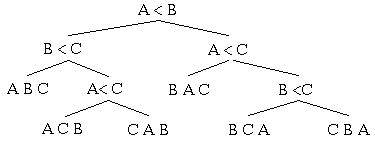
• So we have a tree, with at least n! leaves.
• Consider the best tree that we can buld.
  • It is of height h.
  • This means it has 2^h leaves.
  • Prove this by induction, a tree of height h, has at most 2^h leaves.
  • Again, any path represents the comparisons we must do to sort the list.
  • And h is the number of comparisons.
• So we know that 2^h > n!
  • lg(2^h) > lg(n!)
  • By Stirling's Approximation Proposition A.6, page 659
    • n! > (n/e)ⁿ
  • lg(2^h) > lg((n/e)ⁿ)
  • h > n*lg(n) - n*lg(e);
  • n*lg(n) - n*lg(e) is O(n lg(n))
• This tells us that the height of any decision tree must be at least O(n lg(n))
• Or we need at least O(nlg(n)) comparisons to sort n elements.