Chapter 6, Trees

The Tree ADT

• A nonlinear data structure
  • As we have seen with sots, trees can be used to increase the speed of algorithms.
  • if we can put the data in them correctly
• ubiquitous structures
  • File systems
  • Data bases
  • Web sites
• Relationship:
  • List - before, after
  • Tree - above, below
    Tree - parent, child, sibling, ancestor, descendent
  • Elements are stored heirarchically
  • the first element in the tree is called the root.
  • Every node except for the root has a parent
  • Nodes can also have children
    A tree T is a set of nodes storing elements in a parent child relationship where
    • One node r, is the root of the tree, which has no parents.
    • Each node v in T different from r has a unique parent node u.
    • Our author, using this definition, requires that a tree have at least one node. (IE no empty trees)
    • If u is the parent of v, then v is the child of u
    • If u is the parent of v and w, then v and w are siblings.
    • A node with no children is known as a leaf, or external node
    • Non-leaf nodes are known as internal nodes
    • If there is a path from node u to node v then u is an ancestor of v. Every node is an ascestor of its self.
    • if A = {n in T such that n= ancestor(u)}. A-{u} are the proper ancestors
    • If u is an ancestor of v then v is a descendent of u.
    • A subtree rooted at v consists of all of the descents of v. (including v)
    • 
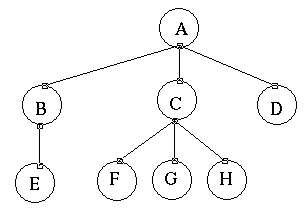
      • A is the root
      • B,C,D are the children of A
      • C is the parent of G
      • {G,C,A} are the ancestors of G
      • {C,A} are the proper ancestors of G
      • F,G and H are siblings
      • {F, G, H} are the propper descendents of C
      • D, E, F, G, and H are leaf nodes
      • A, B and C are internal nodes
    • A tree is ordered if there is a liner ordering defined among the children of each node. (1st child, 2nd child, ...)
    • A binary tree is an ordered tree where each node has at most two children.
    • A proper binary tree is a binary tree where each internal node has two children.
    • In general we label the children as left child and right child.
    • Subtrees are labeled as the left subtree and the right subtree
    • We have seen an example of a decision tree, which is a binary tree.
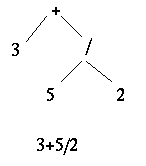
    • Expressions can be respresented by a tree as well.
      • If the node is external, it represents a value
      • If the node is internal, it represents an operation.
      • A tree (and the expression it represents) is evaluated by
        • evaultate the left subtree
        • evaluate the right subtree
        • Perform the operation on the results.
        • Compilers build a parse tree to represent expressions in a language.
        • 
    • Functions for ADT tree
      • The tree holds nodes
      • Operations
        • element(), returns an element at the current position
        • root(), returns the root of the tree ( a position)
        • parent(v), returns the position of the parent of the position v, error if v is the root.
        • children(v), returns an iterator that can traverse the children of node v
        • isInternal(v), isExternal(v)
        • isRoot(v)
        • size() returns the size of a tree
        • elements() - returns an iterator over the elements of a tree these are the objects themselves.
        • positions(), returns an iterator over the nodes of a tree.
        • swapElements(w,v), swap the elements stored at w and v (w and v are positions).
        • replace element(v,e), replace the element at node v with element e
        • Modification functions depend on the type of tree that we are implementing
          • add(e, n), adds element e as child n of the current node.
          • deleteTree(v) makes subtree rooted at v empty
          • Others as we encounter them.