Heaps

• A heap is a binary tree with the two following properties
  • The Heap Order Property
    • In a heap T, for every node v other than the root, the value stored at v is greater than or equal to the value stored at the parent of v
    • 
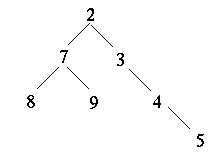
    • This says that the smallest value is stored at the top of the tree.
    • We could reverse this and store the largest at the top.
    • Notice, the heap property is observed for each of the subtrees as well.
    • This makes finding the minimum very easy.
    • It also makes removing the minimum not diffacult
    • How?
  • The Complete Binary Tree
    • A complete tree is a binary tree where the number of nodes is k at each level n, 0 <= n < h, k = 2ⁿ
    • Alternatively: A heap T with height h is a complete binary tree, that is, levels 0, 1, 2, ..., h-1 of T have the maximum number of nodes possible (namely, level i has 2ⁱ nodes, for 0 <= i < h)
    • The above picture does not satisfy this property.
    • This property limits the height of a tree to be O(lg(n))
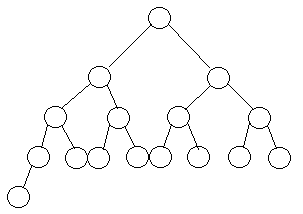
    • We add an additional rule, that all of the external nodes must be to the right of the internal nodes at level h-1
    • It also tells us where to look to find the next empty space where we can put a node.
  • Proposition: A heap containing n nodes has at most height h=ceil(lg(n+1))

    At each level l there are 2l nodes.
    The number of internal nodes (i)  is at least.
    
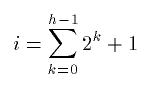    (consider a tree of height 4, level 0, level 1, level 2 are full are full, 
    of internal nodes, and there must be at least one internal node at level
    h-1)
    
    If level h-1 is full, then the sum is 
    
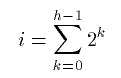    In any case, if a>0 we know
    
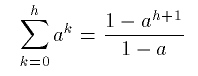    so i = 2h-1
    We know from the previous chapter, the number of external nodes in a proper
    binary tree is one more than the number of internal nodes.
    
    So we know we are between 
    2*(2h-1) <= n <= 2*(2h-1) and 
    2h <= n <= 2h+1 
    So lg(n+1) <= h