Red Black trees

Introduction
- A binary search tree with the following red-black properties
  - Each node is either colored red or black
  - Any non-node is black
  - If a node is red, both of its chldren are black
  - Every simple path from a node to a descendant leaf contains the same number of black nodes.
- The number of black nodes from a node, not including that node, to a NIL node is it's black height.
- bh(x) will be the notation for the black-height of a node.
- We will make the tree a proper tree, or at least consider the missing leaf nodes to be black nodes.
- But we will really just use this to help visualize the tree, every node has a black height of at least one.
- The color of a node can be marked with a single bit.
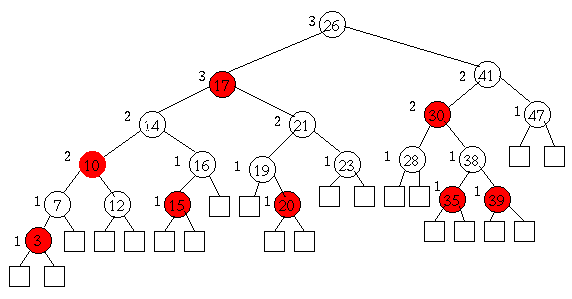
- The black height of the tree is bh(T.root())
- A red-black tree with n nodes (internal) has height at most 2 lg( n +1)
```
Proof:

To do this first show that a tree rooted at x contains at least
    2^bh(x)-1 internal nodes.

By Induction:
Base case:
  Any tree of height 0 is a leaf node, x and has at least
    has bh(x) = 0,  (this is a NIL node)
    2⁰-1 = 1 -1 = 0 internal nodes.

Assume true for all heights less than h.

 Given an internal node, x, with bh(x), at height h
     each child must have either bh(x), or bh(x)-1
     This depends on the color of the child.

     The heights of the children are one less than the height of x
     Therefore by the induction hypothesis, each of the children have

         2^bh(x)-1-1 internal nodes.

	 threfore x has  at least
         2^bh(x)-1-1+ 2^bh(x)-1-1 + 1
       = 2^bh(x)-1 internal nodes.
 
 By property 3 at least 1/2 of the nodes on any path must be black
 There fore the black height of the root must be at least h/2

 n >= 2^h/2-1
 lg(n-1) >=  h/2
 2lg(n-1) >= h
       
```
- The above proof places a bound on the height of a red black tree
- Which also means the time to search a red black tree is bound by O(lg n
- Insertions
  - Like AVL trees, binary search tree insert will unbalence the tree
  - In this case, it will most likely break on of the red-black tree properties
  - As with AVL trees, we will need to fix the tree
  - ```
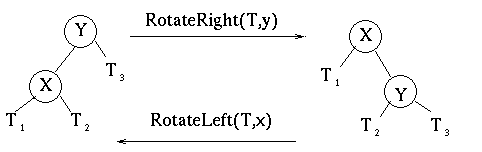
  RotateLeft(T,x)
  ( 1)   y = x.rightChild()
  ( 2)   x.right = y.leftChild()
  ( 3)   if (y.leftChild() != NIL) 
  ( 4)      y.leftChild(y).parent = x
  ( 5)   y.parent = x.parent()
  ( 6)   if x.parent() = NIL
  ( 7)      T.root = y
  ( 8)   else 
  ( 9)      if x = x.parent().leftChild()
  (10)         x.parent().left = y
  (11)      else
  (12)        x.parent().right = y
  (13)  y.left = x
  (14)  x.parent = y
  
     find y
     move T₂ to become x's right child
     reparent things
     move x to be y's right child
  	   
```
- RotateRight is very similar.
- This is O(1)
- Three cases for insert
  - When we insert, the new node is always colored red.
  - This means we may violate only property 3.
  - After we have inserted, we have three cases where the RB tree proper can be violated
  - Case I is where a red node x, has a red parent y and the parent's sibling is also red.
    - In this case, we recolor the parent's parent, and the new node
    - No rotation is required
    - But we may need to change the new node's sibling's color
    - but we have to go up the tree fixing things, since we changed the color of the parent
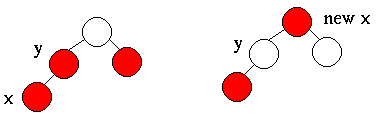
    - Note, x can be the left or right child of y
    - Notice the black height of the two subtrees is preserved.
  - Case II and III occur when the parent's sibling is not red.
    - Case II, the new node is a left child of a parent that is a right child or the node is a right child of a parent that is a left child
    - Rotate to make it a n-child of a n-child n = {right,left}
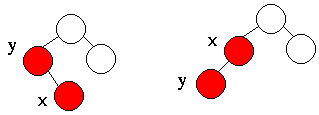
    - This produces case III
    - Case III not case II.
    - Rotate about the new node's parent
    - preserve the color of the root.
    - x (the node under consideration) does not change here (labeled y in the picture because of the rotation)
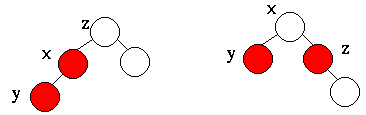
    - Notice again, the black height of each subtree is preserved.
    - Also notice, since the root of the subtree did not change color, the procedure can stop.
    - In all cases, the nodes can all have subtrees atached to them.
    - rotations must account for this (just like AVL trees)
  - Procedure RB-Insert(T,x)
```
( 1)  TreeInsert(T,x)
( 2)  x.color = red
( 3)  while x != T.root() and color x.parent().color == red
( 4)    if x.Parent() = x.parent().parent().leftChild()
( 5)       then  y = x.parent().parent().right
( 6)          if y.color() == red
( 7)              x.parent().color = black   // all case I
( 8)              y.color = black
( 9)              x.parent().parent().color = red
(10)              x = x.parent().parent()
(11)          else if x == x.parent().rightChild()
(12)                 x = x.parent()         // case II
(13)                 LeftRotate(T,x)
(14)              x.parent().color = black  // case III
(15)              x.parent().parent().color= red
(16)              RightRotate(T,x)
(17)    else
(18)       repeat lines 5-16, replace right with left and left with right
(19)  T.root().color = black

	   
```
  - Note, we will travel up the tree
  - But we will only perform two rotations at most.
  - Or a single AVL rotation.
  - So this is O(lg n), and no worse than an AVL tree
- Try with this example
  - Insert(4)
Deleting
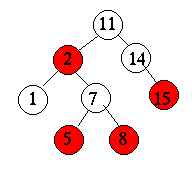
- If we delete a red node, nothing needs to change.
- If we delete a black node, we need to fix the tree
- There are four cases here.
- In each of the four cases
- Just like insert, the only time we must traverse up the tree is when we recolor only
- Or conversely, we stop when we perform a rotation.
- So deleting is better than in an AVL tree.
- We start with the child of the node we just moved up into the tree (x)
- If x's parent is black, and x's sibling is red, rotate x's parent left, which changes case I into one of the other cases.
- If x's sibling is black, recolor x's sibling and move x up the tree. (this reduces the black height of the sibling)
- Otherwise perform a rotation that will balence the tree.
- The routine is just a bunch of special cases like the insert.