Introduction to Transformations.

• The code for today
• I find it really frustrating to use this upside down canvas.
  • It always takes me at least twice to get things into the right location.
  • Then I mess up the sign when moving things.
• By the way, I also would like the center of the canvas to be the origin some time.
• There is a way to fix this.
• To start with, we will be a bit backwards in our logic.
  • We will fix this later.
  • But for now, I will draw things in the "old" canvas coordinate system.
• A reference for the material.
• You could also look at Chapter 17 of the book.
• Representing points
  • We will be doing some linear algebra next.
  • To make things work, we need to change a little about how we think about points.
  • Not too much, but
    • let's just represent a point in two space as [x,y,1].
    • And no matter what, we want to keep that 1 there.
  • We will delay the why for just a bit.
  • If you want some real math theory, you can look into homogeneous coordinates.
• Taking care of the upside down canvas.
  • It would be really nice to have the origin at the bottom of the screen, not the top.
  • We wouldn't have to "flip" the y coordinate all of the time.
• What have we been doing so far?
  • If you think about it, we really need to subtract the y value from the canvas height.
  • 
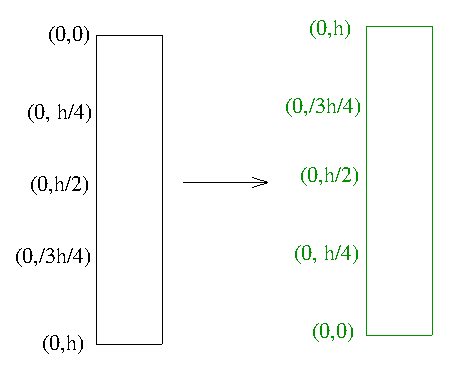
  • For (0,0) we have h-0 = h.
  • For (0,h) we have h-h = 0;
  • For (0,h/4) we have h-h/4 = 3h/4
• So in general if we just subtract the y coordinate from the height, it will draw as if we had an "upside down" canvas.
• By the way, this is just a reflection about the line y=h/2
• But it would be painful to do this to everything we went to draw.
• It turns out that we can use liner algebra to solve our problem.
• Just a quick reminder.
• A point in 2 space is represented as a triple
  • (x,y) => [x,y,1]
• Remember vector matrix multiplication
  • $a = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
  • $T = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$
  • $ T \times a = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \times \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} ax + by + c & dx + ey + f & gx + hy + i\end{bmatrix}$
• Remember matrix matrix multiplication
  • $ A \times B \ne B \times A$
• So what happens if I multiply a point by the matrix
  • $ \begin{bmatrix} x'& y'& 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & h \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
  • $x' = 1x + 0y + 01 = x$
  • $y' = 0x + -1y + 1h = h-y $
  • $ 1= 0x + 0y + 1*1 = 1$
  • So $ \begin{bmatrix} x'& y'& 1 \end{bmatrix} = \begin{bmatrix} x& h-y & 1 \end{bmatrix} $
  • Why do we want that 1 at the end of our coordinates?
• This is such a strong idea, that it is built into most graphics systems.
  • There is a transformation matrix
  • Before a point is drawn, it is multiplied by the transformation matrix to move it to the "proper" location.
• Right now, the transformation matrix is $M = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$
  • So all points are "left alone".
• Transform matrices in the 2d canvas.
  • They do not give access to the full 2d Matrix.
  • $T = \begin{bmatrix} a & c & e \\ b & d & f \\ 0 & 0 & 1 \end{bmatrix}$
• We can also change the transformation matrix (obviously)

  •  ctx.setTransform(1, 0, 0, -1, 0, height); 

  • This will set a,b,c,d,e,f from above.
  • Notice that once I do this, my scene is "flipped".
  • That is nice.
• Just a bit on maintenance of the transformation matrix.
  • The context has the ability to save the current state.

  • ctx.save();

  • And restore the previous value

  •  ctx.restore();

  • The context maintains a history of these matrices in the form of a stack.
    • Save will push the current matrix on the top of the stack.
    • Restore will pop the top of the stack and make that the current matrix.
  • As we will see, this is a relative elegant solution.
• In the demo, there is a cross hair or "axis" that is never impacted by the additional transformations.
• The boxes are potentially effected by two transformations
  • The reflection about the y axis as we discussed.
  • A translation.
• the context supports translate(tx,ty)
  • This is the amount to move each point by.
  • $T = \begin{bmatrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{bmatrix}$
  • $ \begin{bmatrix} x'& y'& h' \end{bmatrix} = \begin{bmatrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
    • $x' = 1x + 0y + 1tx = x + tx$
    • $y' = 0x + 1y + 1ty = y + ty$
    • $h' = 0x + 0y + 1*1 = 1 $
  • Once again, note why we have the extra 1 in the coordinate system.
• We might want to put the text back the right way.
  • This will be counter intuitive as the text is drawn "correct" for the default canvas.
  • We will need to "flip" the text, but only the text.
  • So before we draw the text we save the state.
  • Flip the text
  • Restore the state.
• Flipping the text can be done with a scale matrix.
  • $S = \begin{bmatrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{bmatrix}$
  • $ \begin{bmatrix} x'& y'& h' \end{bmatrix} = \begin{bmatrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$
  • $x' = sx \times x $
  • $y' = sy \times y $

• ctx.scale(sx,sy); 

• Because we are changing systems, I computed the y location of the text by hand,