Simple Collisions

• Accurate 3D collision detection of arbitrary objects is a difficult thing to do.
  • I believe that there is still active research in this area.
  • Recent publications
• Fortunately, for most of you Unreal handles this for you.
  • The default objects have onCollisionEvents which you can handle
    Take a look.
    • Or the default is usually reasonably good.
  • My goal is not to do research level, but just gain a basic understanding.
  • Circles are by far the easiest thing.
    • Given circle $c_1$ of radius $r_1$ and circle $c_2$ of radius $ r_2$, how can you tell if the two have "collided"?
      • if distance($c_1, c_2$) ≤ $r_1+r_2$
    • Look at circle.html
  • For this reason, sometimes a system will put everything inside of a "bounding circle".
    • The system does a preliminary bounding circle check
    • If that fails, then a more detailed check is performed.
  • What about a circle and a line?
    • Assume the line is vertical
      • 
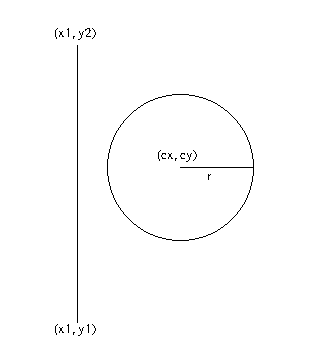
      • if $y_1 \le c_y \le y_2$
        • $d = |c_x - x_1| $
      • if $y1 > c_y$
        • $d = $ distance( $(c_x, c_y), (x_1, y_1) $ );
      • else
        • $d = $ distance( $(c_x, c_y), (x_1, y_1) $ );
      • Then check if the distance is greater than r.
    • Can you do the same for horizontal?
    • How about a line segment in general?
      • You can compute the point $(x_i, y_i)$ where a point $(x_c, y_c)$ is closest to a line segment $(x_1, y_1), (x_2, y_2)$
      • $y_1 \ne y_2 $ and $ x_1 \ne x_2$
      • 
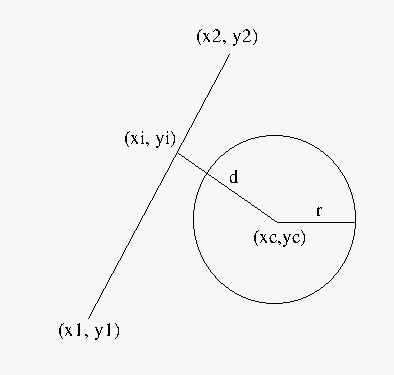
        • $m = \frac{y_2-y_1}{x_2-x_1} $ and $b = y_1-mx_1$
        • The line from $(x_c, y_c)$ to the segment intersects at $(x_i, y_i)$.
        • The slope of that line will be $-\frac{1}{m}$
        • And the equation of the line will be $ y = \frac{x_c -x}{m} +y_c $
          • $y-y_1 = m(x-x_1)$ point slope form
          • $y - y_c = -\frac{1}{m} (x-x_c) $ Put $(x_c, y_c) $ in for $(x_1,y_1)$
          • $y = \frac{-(x-x_c)}{m} + y_c$
          • $y = \frac{(x_c-x)}{m} + y_c$
      • So at the point $(x_i, y_i)$
        • $y_i = \frac{x_c-x_i}{m} + y_c$, the equation for the first line
        • $y_i = mx_i + b$ the equation for the second line
      • so
        • $ mx_i + b = \frac{x_c-x_i}{m} + y_c$
        • $m^2x_i + mb = x_c - x_i + my_c$
        • $m^2x_i + x_i = x_c -mb +my_c $
        • $x_i(m^2 + 1) = x_c -mb +my_c $
        • $x_i = \frac{x_c -mb +my_c}{m^2+1} $
      • and putting this int o $y=mx+b$
        • $y_i = m\frac{x_c -mb +my_c}{m^2+1} + b $
      • So you can check to see if
        • $x_1 \le x_i \le x_2$ and $y_1 \le y_i \le y_2$
          • Check the distance from $(x_c, y_c) $ to $ (x_i, y_i) $
        • Otherwise check the distance to the closest end point.
      • This could be optimized but yuck.
    • We like nice horizontal and vertical lines.
  • What about a circle and a rectangle?
    • An inside test is easy.
    • How about an outside test?
      • Could we just check the distance to the four corners?
        • Think long skinny rectangle.