Collision With a Line

• What about a circle and a line?
  • Assume the line is vertical
    • 
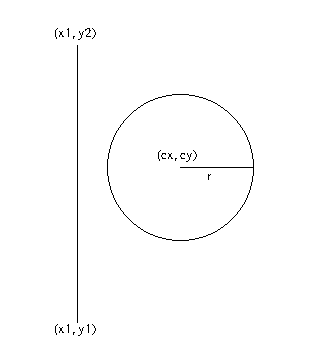
    • if $y_1 \le c_y \le y_2$
      • $d = |c_x - x_1| $
    • if $y1 > c_y$
      • $d = $ distance( $(c_x, c_y), (x_1, y_1) $ );
    • else
      • $d = $ distance( $(c_x, c_y), (x_1, y_1) $ );
    • Then check if the distance is greater than r.
  • Can you do the same for horizontal?
  • How about a line segment in general?
    • You can compute the point $(x_i, y_i)$ where a point $(x_c, y_c)$ is closest to a line segment $(x_1, y_1), (x_2, y_2)$
    • $y_1 \ne y_2 $ and $ x_1 \ne x_2$
    • 
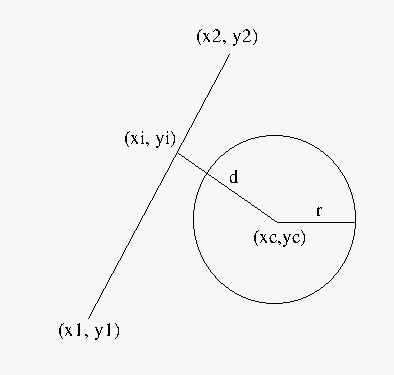
      • $m = \frac{y_2-y_1}{x_2-x_1} $ and $b_1 = y_1-mx_1$
      • The line from $(x_c, y_c)$ to the segment intersects at $(x_i, y_i)$.
      • The slope of that line will be $ -\frac{1}{m}$
      • And the equation of the line will be $ y = \frac{x_c -x}{m} +y_c $
        • $y-y_1 = m(x-x_1)$ point slope form
        • $y - y_c = -\frac{1}{m} (x-x_c) $ Put $(x_c, y_c) $ in for $(x_1,y_1)$
        • $y = \frac{-(x-x_c)}{m} + y_c$
        • $y = \frac{(x_c-x)}{m} + y_c$
    • So at the point $(x_i, y_i)$
      • $y_i = \frac{x_c-x_i}{m} + y_c$, the equation for the first line
      • $y_i = mx_i + b_1$ the equation for the second line
    • so , set the two equal and solve for $x_i$
      • $ mx_i + b = \frac{x_c-x_i}{m} + y_c$
      • $m^2x_i + mb = x_c - x_i + my_c$
      • $m^2x_i + x_i = x_c -mb +my_c $
      • $x_i(m^2 + 1) = x_c -mb +my_c $
      • $x_i = \frac{x_c -mb +my_c}{m^2+1} $
    • and putting $x_i$ into $y=mx+b$
      • $y_i = m\frac{x_c -mb +my_c}{m^2+1} + b $
    • So you can check to see if
      • $x_1 \le x_i \le x_2$ and $y_1 \le y_i \le y_2$
        • Check the distance from $(x_c, y_c) $ to $ (x_i, y_i) $
      • Otherwise check the distance to the closest end point.
    • This could be optimized but yuck.
  • We like nice horizontal and vertical lines.
• Take a look a line demo