- Remember, this is filling an width by height array.
- Integer indexes please
- We have two endpoints
- And an operation WritePixel(ix,iy,value)
- A pixel at (0,0) is actually drawn at (1/2,1/2)
- But for now, just go with square pixels, integer indexes.
- This is the algorithm graphics cards use
- Invented in 1962 by Jack Bressenham
- Published in 63
- Big Ideas
- Do all integer calculations
- "predict" an integer error for the axis of minor change
- Move when this error becomes too large.
- WLOG assume $0 \le m \le 1 $
- You can flip the role of x and y if this is not the case.
- Given (x1,y1) and (x2, y2) $$ \begin{array}{rcl} y & =& mx + b \\ & = & \frac{\Delta y}{\Delta x} \cdot x + b \\ \Delta x \cdot y & = & \Delta y \cdot x + \Delta x \cdot b \\ 0 & = & \Delta y \cdot x - \Delta x \cdot y + \Delta x\cdot b \\ \end{array} $$
- Let $A = \Delta y, B = -\Delta x, C = b \Delta x$
- $F(x,y) = Ax+By+C = 0$
- Note, this is entirely an integer computation.
- Example: A line from (0,2) to (30,12)
- $m = \frac{12-2}{30-0} = \frac{10}{30} = \frac{1}{3}$
- $b= 2$
- y = 1/3 x + 2
- m = 1/3
- $\Delta x = 3$
- $\Delta y = 1$
- b = 2
- m = 1/3
- We can find A, B and C
- $A = \Delta y = 1 $
- $B = -\Delta x = -3 $
- $C = b\Delta x = 3*2 = 6 $
- So $F(x,y) = x -3y + 6$
- When $F(x,y) = 0$, a point is on the line.
- (0,2) is on the line since 0-6+6 = 0
- (3,3) is on the line since 3-3*3+6 = 0
- And also, if a point is not on the line if it is above or below the line.
- (3,4) is above the line 3-3*4+6 = -3 < 0
- (3,1) is below the line 3-3*1+6 = 6 > 0
-
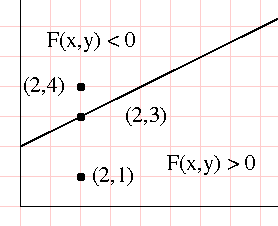
- Example: A line from (0,2) to (30,12)
- Assume we are drawing a line from $(x_1,y_1)$ to $(x_2,y_2)$.
- We know that$ F(x_1,y_1)$ is on the line.
- The next point will be $F(x_1+1, y_1)$ or $F(x_1+1, y_1+1)$, we just need to decide which.
- Remember, the slope is less than one, so the next x will just be to add one.
- Determine this by evaluating $F(x_1+1, y_1+1/2)$
- If $F(x_1+1, y_1+1/2)$ is positive, the line is above it, select $(x_1+1, y_1+1)$
-
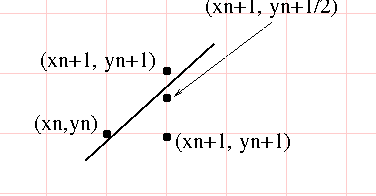
- If $F(x_1+1, y_1+1/2)$ is negative, the line is below it, select $(x_1+1, y_1)$
-
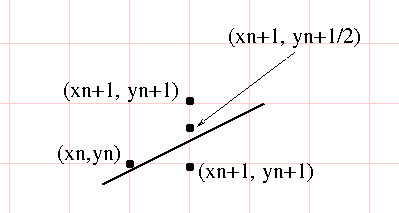
- Notice, this involves one point computation, and one difference computation, not two.
- Define $D = F(x_1+1, y_1+1/2) - F(x_1,y_1)$
- This tells us how much the error changes from the current point to the predictor for the next point. $$ \begin{array}{rcl} D &=& F(x_1+1, y_1+1/2) -F(x_1,y_1) \\ &=& A(x_1+1) + B(y_1+1/2) + C - (Ax_1 +By_1+C) \\ &=& Ax_1 - Ax_1 + A + By_1 - By_1 + 1/2B +C-C \\ &=& A + 1/2 B \\ \end{array} $$
- D will give us the same indication as before.
- Since $(x_1,y_1)$ is on the line, $F(x_1, y_1) = 0 $
- So we initialize D to be 0
- The starting point has no error
- The first point will be off by $A + 1/2 B$ or $ (\Delta y-1/2\Delta x) $
- For our example line (y = 1/3 x + 2) starting at (0,2)
- A = 1, B = -3, C = 6
- (0,2) is on the line.
- F(1,2.5) = 1 - 3*2.5 + 6 = 1 - 7.5 + 6 = -0.5
- This is negative, so it is above the line, so the point is (1,2)
- $$ \begin{array}{rcl} D& =& F(1, 2+1/2) - F(0,1) \\ & =& 1 + 1/3(-2) \\ & =& -1/3 \\ \end{array} $$
- Again, this is negative, so choose (0+1,2)
- This makes sense, as the change is only 1/3
- The next difference will be either
- If D was negative in the previous step $$ \begin{array}{rcl} \Delta D & = & F(x1+2, y1+1/2) - F(x1+1,y1+1/2) \\ & = & A(x1 + 2) + B(y1+1/2) + C - A(x1+1) - B(y1+1/2) - C \\ & = & Ax1 + 2A - Ax1 - A \\ & = & A \\ & = & \Delta y \\ \end{array} $$ If D was positive in the previous step $$ \begin{array}{rcl} \Delta D & = & F(x1+2, y1+3/2) - F(x1+1,y1+1/2) \\ & = & A(x1+2) + B(y1+3/2) + C - A(x1+1) - B(y1+1/2) - C \\ & = & Ax1 + 2A + By1 +3/2B + C - Ax1 - A - By1 -1/2B - C \\ & = & A+B \\ & = & \Delta y - \Delta x \\ \end{array} $$
- So we need to change D by adding $\Delta y$ or by adding $\Delta y-\Delta x$
- So for our example
- The second calculated point on the line :
- The last D = -1/3 was negative, (at (1,2))
- so the next D = -1/3 + 1 = 2/3
- This is positive, so the line is below (2,2.5) so choose (2,3)
- F(2,3) = 2 + -3*3 + 6 = -1, which is above the line by 1
- F(2,2.5) = 2 - 7.5 + 6 = .5 which is below the line by .5
- F(2,2) = 2 + -2*3 + 6 = 2 which is below the line.by 2
- So (2,3) is the closer of the two points to the line.
- The next point
- The last D = 2/3 was positive so
- The next D = D + Δy - Δx, = 2/3 + 1 - 2 = -1/3
- This is negatvie so the line is above (3, 2.5) so choose (3,3)
- And so on.
- The second calculated point on the line :
- But we really don't care about the value of D, just the sign.
- So we can multiply everything by 2, and deal with d = 2D
- d0 = 2Δy - Δx
- dn = dn-1+2Δy when dn-1 < 0;
- dn-1+2Δy-2Δx, when dn-1 > 0.
- So the algorithm is
dx = x2 - x1 dy = y2 - y1 d = 2*dy - dx y = y1 x = x1 while x <= x2 WritePixel(x,y,c) if d > 0 y = y + 1 d = d - 2*dx end if d = d + 2*dy x++