2.1.2 (Real-number Coordinate Systems) or Translating between 2D Coordinate Systems

• The book section.
• Our goal for the notes.
• I will do things somewhat different than he does.
  • ie He gives formulas
  • I want to think about where these come from.
• I am going to work in regular coordinates, not flipped like the canvas.
  • Flipping is not hard and we will discuss that later.
• If we have modeled a scene in the coordinate system $o_{min} = (o_l, o_b)$ to $o_{max} = (o_r, o_t)$.
• Take a look at the picture at the bottom of the page, or the goal for today. Either will do.
• And we want to transform it to another space, say $n_{min} (n_l, n_b)$ to $n_{max} = (n_r, n_t)$.
  • It would be nice to come up with a formula to move the points
  • Transform(point, oMin, oMax, nMin, nMax) that moves the point from the modeling coordinate system to the viewing system.
• My general strategy
  1. Move the original window to the origin.
  2. Scale it to the "unit" window
  3. Scale it to the "new" window.
  4. Move this new window to the correct location.
• For an arbitrary point, $p_{old} = (x_{old},y_{old})$,
• Step 1, move the original to the origin.
  • We will simply subtract: $p_1 = p - o_{min}$
  • Note this moves:
    • $o_{min}$ to $(0,0)$
    • $o_{max}$ to $o_{max}'(o_l-o_r,o_b-o_t)$
• For step 2, I need to scale this box the "unit" box.
  • Simply divide by $o_{max}'$
  • $p_2 = \frac{p_1}{o_{max}'}$
• For step 3, we need to scale the scene to the new size.
  • let $n_{max}' = (n_r-n_l, n_t-n_b)$
  • And $p_3 = p_2*n_{max}'$
• Finally, we need to move the window to the right location.
  • This is simply adding $n_{min}$
  • $p' = p_3 + n_{min}$
• Unrolling this we get
• $p' = \frac{p_{old}-o_{min}} {o_{max}'} * n_{max}' + n_{min}$
• This one matches the book:
• $x' = (x_{old}-o_l)\frac{n_r-n_l}{o_r-o_l} + n_l$
• The book exchanges top and bottom to deal with the "upside down" window system.
• $y' = (y_{old}-o_b)\frac{n_t-n_b}{o_t-o_b} + n_b$

Consider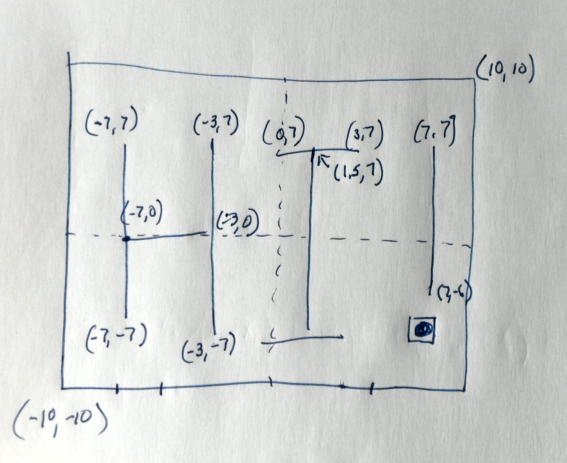

• The modeling coordinates are (-10,-10) to (10,10)
• The viewing coordinates are (150,150) to (300,300)
  • But we could edit the code to make them whatever we wish.