The Pinhole Camera

• This might help today.
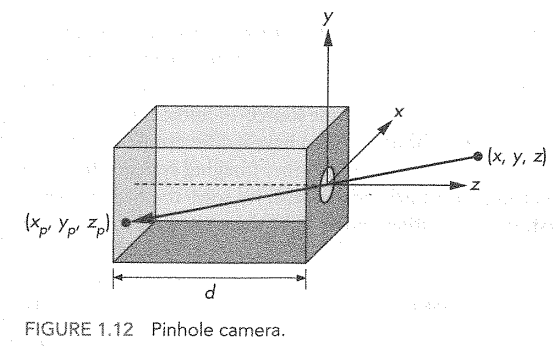
• The Pinhole camera
  • Is a box with photographic material on the back wall.
  • There is a pinhole in the center of the front.
    • Let's consider the pinhole to be (0,0,0).
    • The back wall is at -d
    • 
    • We are looking along the positive "z" axis
    • And we are looking at a point (x,y,z) in space.
  • Notice, the photographic material is centered at (0,0,-d)
• Light will travel from the point (x,y,z)
  • Through the pinhole
  • And "strike" the photo at $(x_p, y_p, z_p)$
• Let's assume we know the "color" of point, what pixel should we set to that color
  • IE, where is $(x_p, y_p, z_p)$
  • $z_p$ is -d by definition
  • For simplicity, assume $x=0$
  • We have something like this
  • 
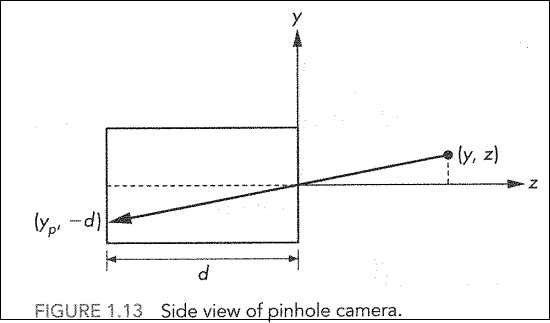
  • In this case, we know $(0,y, z)$, the point projected into the yz-plane
  • 
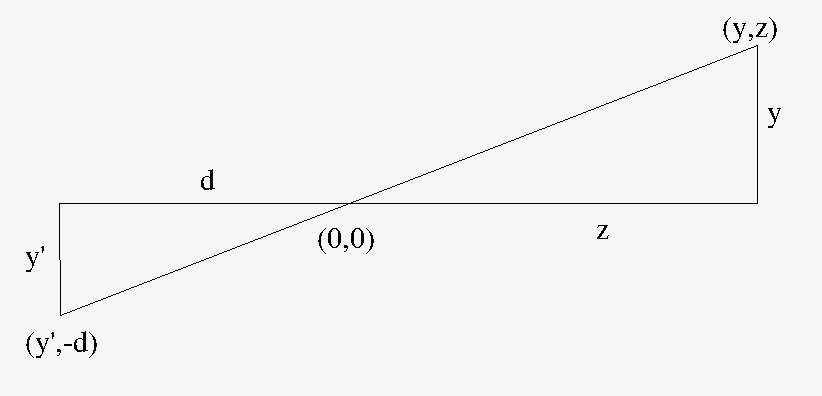
  • We know $z_p = -d$
  • We can use similar triangles to compute $y_p$.
  • $\frac{y_p}{-d} = \frac{y}{z}$
  • $y_p = \frac{y}{z}\times -d$
  • $y_p = -\frac{y}{\frac{z}{d}}$
• The same is true for $x_p$
  • ie $x_p = -\frac{x}{\frac{z}{d}}$
• So the new position will be $(-\frac{x}{\frac{z}{d}}, -\frac{y}{\frac{z}{d}}, -d)$
• A modification is to move the "photographic plate " to in front of the camera.
• 
• The new position will then be $(\frac{x}{\frac{z}{d}}, \frac{y}{\frac{z}{d}}, d)$
• We can develop the matrix $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{d} & 0 \end{bmatrix}$
  • This matrix needs to be applied AFTER all of the other transformations have been accomplished.
  • Later we will call this the Projection matrix.
  • This is because it projects the points from three space to two space.
• Notice that all points along the line $(x,y,z) , (x_p, y_p, d)$ are projected to the same point.
  • If we keep track of depth, we can decide which to display/store in the frame buffer..
• A second parameter, the "height" h of the photographic plate controls the view angle
  • Again a projection into the YZ plane.
  • 
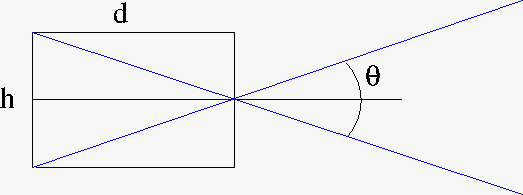
  • $\tan(\theta) = \frac{opposite} {adjacent}$
  • opposite = $\frac{h}{2}$
  • adjacent = $d$
  • $ \tan(\frac{\theta} {2}) = \frac{\frac{h}{2}}{d} $
  • $ \tan(\frac{\theta} {2}) = \frac{h}{2d} $
  • In this case $\theta = 2 \tan^{-1}(\frac{h}{2d})$
  • The same calculation is true for x.
    • But for non-square "photographic plates" we will have different angles.
  • The same is true for the modified camera
  • 
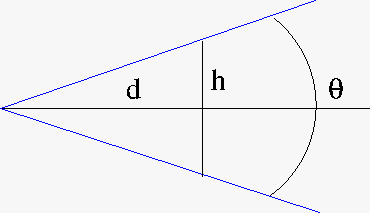
• We will further develop these ideas, but in general
  • you can change d,
  • you can change h (and w)
  • you can change the alignment of the "photographic plate"
    • Location in space
    • Angles.
• We normally add a back plane
  • This allows us to throw away things that are "too far away"
  • This forms the view frustum.
• What would the projection matrix $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$ do?
  • orthographic
  • perspective