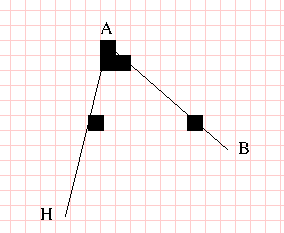Polygon Scan Conversion

• We know how to draw lines
• We know how to clip polygons.
• We just need to finish filling polygons and we are done with rasterization.
• This is part of chapter 8
• Triangle conversion.
  • This is called scan line conversion
  • A polygon method exists for this, but it is more complex.
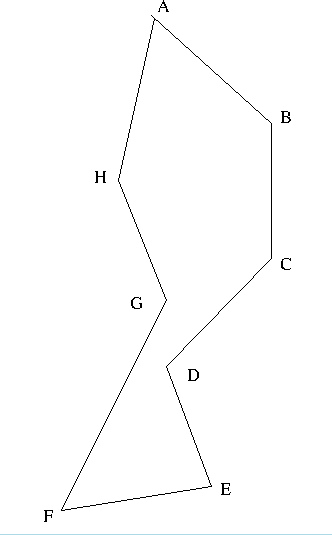
  • Consider this polygon
    • 
  • Have a list of edges.
    • AB, BC, CD, DE, EF, GF, HG, AH.
  • Sort the edges by maximum y coordinate.
    • AB, AH, BC, HG, CD, GF, DE
  • Start at the maximum y value.
  • Add any edges with this value to the active list.
    • AB and AH
  • Run Bresenhams on each of these, but keep track of when Y changes.
    • For each active line, keep
    • x,y, dx, dy, D (the parameters of Bresenham's)
  • Sort them by minimal x value of the active point.
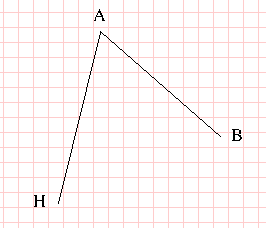
    • So we will draw from AH to AB
  • Perform a simple fill between these points.
  • 
  • 
  • 
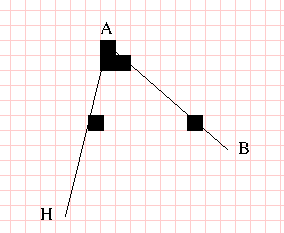
  • As Y changes, check the list to see if a new line is added or one drops out.
  • 
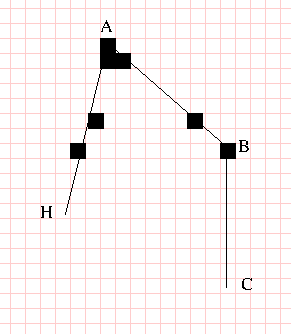
  • Stop when you get to minimal y.
  • Notice, you can interpolate other items as you go.
  • What do you do if it is not a simple polygon
  • 
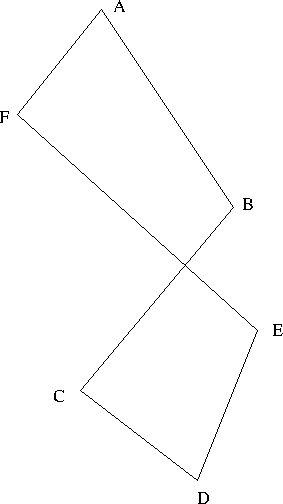
    • Converting AF - AB will be fine.
    • But somewhere in the middle of FE - BC the order will switch to be BC - FE
    • We can scan convert complex polygons, but it adds a complexity to the algorithm.
  • This could get messy for arbitrary polygons.
  • But everything is nice and clean for triangles.
    • No lines crossing.
    • Only two active edges at any point in the conversion.
• What about more complex polygons?
  • To simplify things
    • Horizontal lines are removed completely.
    • Endpoints are foreshortened by 1 in the Y direction for the lower y endpoint.
  • 
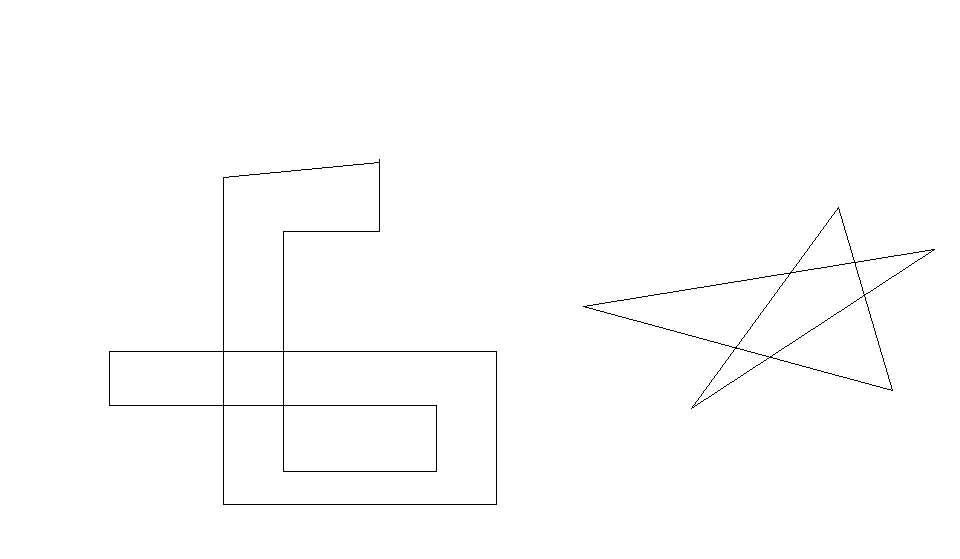
  • The Even Odd winding rule
    • Initialize the count to 0
    • Every time we cross an edge add 1 to the count.
    • Fill from Odd to even, not even to odd.
    • Inflection points count as one change.
    • Local max/min count as two changes.
  • 
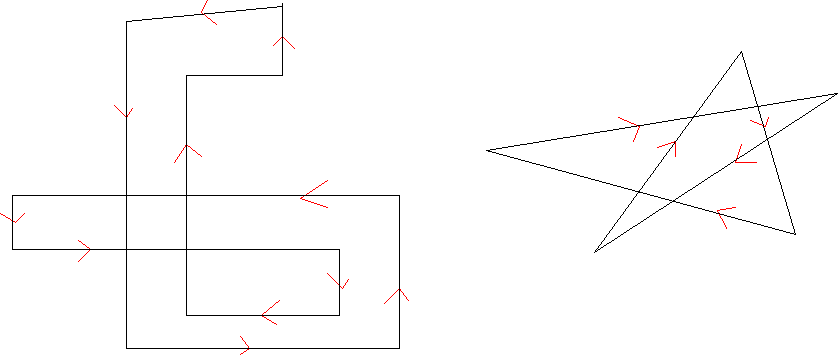
  • The Nonzero winding rule
    • Initialize the count to 0
    • Each time a line goes from top to bottom, add 1
    • Each time a line goes from bottom to top subtract one.
    • Fill when non-zero
• What about something we don't have "hard" edges for.
  • FloodFill
  • Various algorithms, same idea.
  • You need
    • A connected boundary.
    • A starting point.
    • A fill color.
    • A background color to fill, or an edge color, or ...
  • an example