Intro to Lighting

• This is chapter 6 of the book.
• We discussed this intro before
  • It is impossible with what we know now to do light and color accurately.
    • Light emits from a source and bounces around until it strikes your eyes.
  • And until very recently, it was not possible to do the next best thing
    • Raytracing
    • Trace a light ray back from the pixel into the scene until it strikes a light source.
    • NVIDIA Claims that they can do real time ray tracking right now.
      • Between 6GigaRays/sec and 10GigaRays/sec
      • I think we should investigate raytracing next.
    • Looks like they are $1K or so.
• So putting the $1K cards aside, how have we traditionally done lighting/color?
  • We fake it with three components.
    • Ambient light is the fake factor.
      • This is just the "filler light" in the scene.
      • It is sort of the roundoff error.
    • Specular reflection
      • The light that directly bounces off a surface.
      • Mostly for smooth surfaces.
    • Diffuse reflections
      • The light that is scattered by a surface.
      • Mostly rough surfaces.
• We fake lights as well
  • As before, we generally consider point light sources.
  • They radiate light of a given "color".
  • We will model a light source as
    • A position (x,y,z)
      • This will need to be transformed from modeling to camera coordinates
    • A color or intensity for light l
      • $L_l = \begin{bmatrix} L_r \\ L_g \\ L_b \\ \end{bmatrix} $
    • Intensity and Distance
      • The intensity of the light should fade as we move away from a light source.
      • The intensity is inversely proportional to the distance from the light source to the object.
      • Assume $p_l$ is the location of the light source, and $p$ is the location of the item.
      • $L(p,p_l) = \frac{1}{|p-p_l|^2}L_l$
      • In practice the following model is used
        • $d = |p-p_l|^2 $
        • $L(p,p_l) = \frac{1}{a + bd + cd^2}L_l$
        • a,b and c are constants chosen to produce the "right" light
        • Ie they are attributes selected based on artistic principles.
    • If we continue, we will add additional properties such as direction, and spotlight parameters.
  • Ambient light is consistent throughout the scene
    • $L_a = \begin{bmatrix} L_{ar} \\ L_{ag} \\ L_{ab} \\ \end{bmatrix} $
    • Or we can make a per light ambient value
      • And if we turn a light off, that ambient component is removed.
    • For now, let's just consider $L_a$ as a constant.
• Surfaces
  • We could do a full physical simulation of surfaces.
  • But as you might have guessed, this would be too expensive.
  • So we model surfaces as three values.
    • $R_a = \begin{bmatrix} R_{r} \\ R_{g} \\ R_{b} \\ \end{bmatrix} $
    • $R_s = \begin{bmatrix} R_{r} \\ R_{g} \\ R_{b} \\ \end{bmatrix} $
    • $R_d = \begin{bmatrix} R_{r} \\ R_{g} \\ R_{b} \\ \end{bmatrix} $
  • Each surface will have these values.
  • They will probably be uniform values for each surface.
  • They are selected to "model" the surface properties.
• Based on the intensity of light i ($L_i$) and the surface properties $R$ we will compute $I_i$ at a given point.
  • This will consist of RGB components for Specular, Diffuse and Ambient light
• The intensity at any point will be modeled
  • $I_p = \Sigma_l (L_aR_a + L_dR_d + L_sR_s)$
  • Ie add up the individual components for each light.
• But what are the component computations?
• Ambient light
  • $I_a = L_a * R_a$
  • Again, we can look at this globally
    • $L_a$ is a constant for the room.
    • $R_a = k_r, k_g, k_b$ a constant for all surfaces.
  • Or locally
    • Each light has a $L_a$
    • Each surface has a $R_a$
  • Or some mixture.
• Diffuse light.
  • We model light after Lambert's reflectance model.
  • $I_d = L_d R_d cos(\theta)#
  • or
  • $I_d = l \cdot n L_d R_d$
  • Where $l$ is the incoming ray of light
    • Or a vector pointing from the light to here.
    • If we know the position of the light and the fragment this is easy to compute
    • $p_l - p$
  • $n$ is a surface normal
  • 
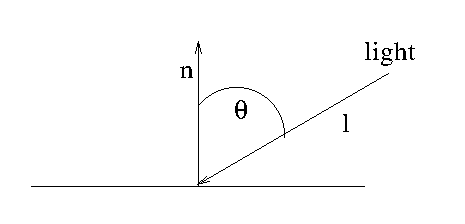
  • So $cos(\theta) = l \cdot n$
  • And there is a dot operation in glsl.
  • Note as the angle $\theta$ gets larger, less light is reflected.
  • But $l \cdot n$ might be negative.
    • When would this occur?
    • max($l \cdot n$, 0) will handle this just fine.
• Surface Normals
  • How can you compute a surface normal?
  • How about a vertex normal?
  • $n_v = \frac{1}{|s|} \Sigma_s n_s$
    • Where s is the set of surfaces.
    • $n_s$ is the surface normal for surface s.
  • Where can we compute this?
• The equation so far
  • $I = L_a R_a + \frac{1}{a+bd+cd^2} max((l\cdot n),0) L_d R_d$
• Diffuse Light.
  • Phong modeled specular light with
  • $I_s = L_s R_s cos^\alpha \phi$
  • $\phi$ is the angle between the viewer and the outgoing light.
  • 
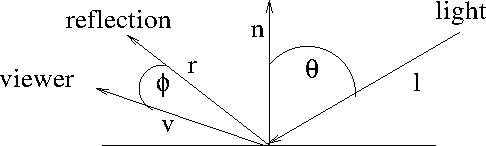
  • Notice, cos falls off as the angle gets larger.
  • $-1 \le cos\phi \le 1 $
  • So $ cos(\phi)^\alpha$ will get smaller for higher values of $\alpha$
  • $cos(\phi) = r\cdot v$
  • $I_s =L_s R_s max((r\cdot v)^\alpha,0)$
• The full Phong model
  • $I = L_a R_a + \frac{1}{a+bd+cd^2} (max((l\cdot n),0) L_d R_d + max((r\cdot v)^\alpha,0) L_s R_s)$
  • Relies on the surface normal being interpolated as we move across the surface.
• Phong-Blinn
  • recalculating $r \cdot v$ is expensive at every point.
  • Blinn proposed to compute a constant half angle instead.
  • 
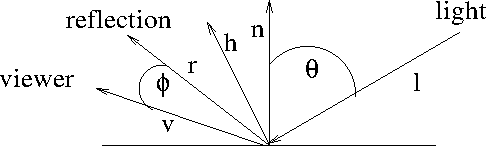
  • This angle is halfway between the viewer and the light source.
  • $h = \frac{l+v}{|l+v|}$
  • This will serve as a good constant approximation
  • So $r\cdot v$ is replaced with $n\cdot h$
  • With an appropriate substitution for $\alpha$
  • $I = L_a R_a + \frac{1}{a+bd+cd^2} (max((l\cdot n),0) L_d R_d + max((n\cdot h)^\alpha,0) L_s R_s)$