Some Math

• We will generally think of things as vectors.
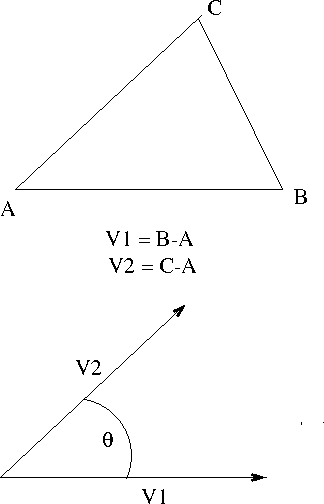
• Given a triangle, we can convert it to vectors
  • 
• The magnitude of a vector
  • v₁ = (x₁, y₁ , z₁)
  • |v₁ = sqrt(x₁², y₁² , z₁²)
  • Note in MV.js this is called length.
  • By the way, there is a function that "normalizes" a vector
  • normalize in MV.js
  • v' = v/|v|
  • This will be very useful (in the next set of notes).
• The dot product of two vectors
  • v₁ = (x₁, y₁ , z₁)
  • v₂ = (x₂, y₂ , z₂)
  • v₁· v₂ = x₁ x₂ + y₁ y₂ + z₁ z₂
  • This is a scalar.
  • It can be interpreted as
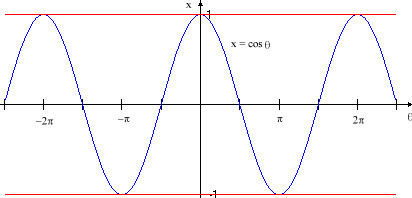
  • v₁· v₂ = |v₁| |v₂| cos (Θ)
  • So if |v₁| = 1 and |v₂| = 1
  • v₁· v₂ = cos(Θ)
  • Note in MV.js this is called dot
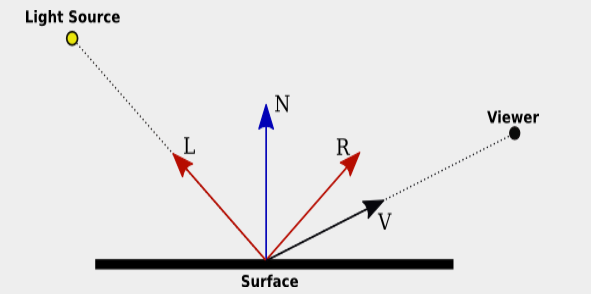
• So given a normal to a triangle
  • Given an eye position
  • 
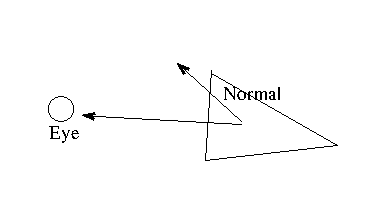
  • We can compute the angle between the normal and the vector towards the eye.
  • If cos(Θ) > 0, we can see the front of the triangle
  • If cos(Θ) < 0, we can see the back of the triangle
  • Remember cos(Θ)
  • 
  • The book, sanely, derives this the
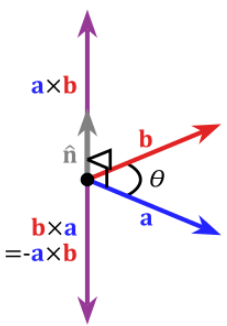
• The Cross product
  • This works in three space, but does not generalize to n space.
  • v₁ × v₂ = |v₁||v₂ |sin(Θ)
  • v₁ × v₂ = (y₁z₂-z₁y₂, z₁x₂ - x₁z₂, x₁y₂ - y₁x₂)
  • Or more useful, v₁ × v₂ = u, the normal to the v₁ × v₂ plane.
  • 
  • In MV.js there is a cross function.
• So why talk about this now?
  • It is important so we understand backface removal
• For flat shading
  • We provide a uniform color across a surface.
  • But it depends on the lights in the scene.
  • 
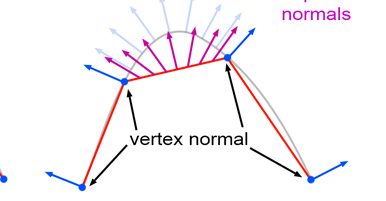
• For smooth shading
  • We start with vertex normals.
  • These are interpolated across the surface
  • 
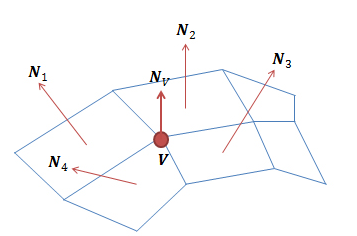
• Computing vertex normals
  • Really just the average of associated surface normals.
  • 
  • So we can calculate these in our conversion from OFF to JS
  • Assume all polygons are given in CW or CCW
  • Probably provide a command line argument to reverse the normal computation.