• We begin looking at raster techniques.
  • I am using Angle's fifth edition for these notes.
  • This mostly assumes that we have a PlotPixel(int x, int y, color c) command that will plot a pixel of the given color.
    • We may later assume that we have a color GetPixel(int x, int y) routine which returns the color value of a pixel set in the frame buffer.
    • We also have a way to clear the frame buffer.
  • The input to a rasterizer?
    • Primitives such as lines, polygons, ...
  • The output of rasterization is a series of fragments
    • These are values in screen coordinates.
    • They have attributes such as color, depth, ...
    • We will see more of fragments later.
    • Fragments might have real coordinates
    • But they will be changed to integer values eventually.
  • Turning fragments into pixels, pixels are assumed to be centered at positions half way between the integer (like we do in our canvas)
  • Line Drawing
    • We will draw a lot of lines.
    • We need line drawing to be
      • Quick
      • Accurate.
        • Include both endpoints.
        • Otherwise our polygons will have holes.
    • Brute Force
      • m = (y-y1)/(x-x1)
      • Becomes y = y1 + m(x-x1)
      • There is a problem if x1==x2
      • But also problems if m>1
      • And some nasty floating point problems.
      • Oh ya, and will there be holes? 
            BruteForce: function() {
        var x,y;
        var m;

        if (this.x1 == this.x2) {
           for(y =Math.min(this.y1, this.y2); y <= Math.max(this.y1,this.y2)
                                              ; y++) {
             this.PlotPoint(this.x1, y);
           }
        } else  {
           m = (this.y1-this.y2)/(this.x1-this.x2)
        }

        for(x=this.x1; x<=this.x2; x++) {
           y = Math.floor(this.y1 + m * (x-this.x1));
           this.PlotPoint(x,y);
        }
        return;
    },
    • DDA
      • Digital Differential Analyzer.
      • WLOG assume 0 ≤ |m| ≤ 1
        • this means that x is the major axis of change
        • Or x changes by 1 each time and y changes by less than 1.
        • So no holes.
      • Also assume (or force to be true) xstart < xend. 
        We know that ya   = y1 + m(xa - x1)
             ya+1 = y1 + m(xa+1 - x1)
	          = y1 + m(xa+1 - x1)  Because xa+1 = xa  + 1
          so ya+1-ya  = y1 + m(xa+1 - x1) - [y1 + m(xa - x1)]
	              = m
      • In other words, each time we change x by 1, we change y by m 
      •         dx = this.x2-this.x1;
        dy = this.y2-this.y1;
        m = dy/dx;
        if (Math.abs(dx) >= Math.abs(dy)) {
            y = this.y1;
            for(x=this.x1;x<= this.x2;x++) {
               this.PlotPoint(x,y);
               y = y+m;
            }
        }
      • Did we gain anything computationally? 
      •                //DDA
               y = y+m;
	       // Brute Force
               y = Math.floor(this.y1 + m * (x-this.x1));
      • Note, we do have to keep y as a float.
        • Consider the case where m = 1/4
        • We need to accumulate the 1/4 four times for y to change.
      • So there is still some nasty floating point math, but far less.
      • And actually, any person with any math knowledge would be able to do this optimization.
      • What would we have to do for |m| > 1?
    • Bresenham's
      • Invented in the early 60s at IBM
      • By Jack Bresenham
      • Again we will assume that xstart < xend
      • WLOG assume 0 ≤ |m| ≤ 1
      • As we stated before, the center of a pixel is at (x+1/2, y+1/2) 
        
At an arbitrary step i, we have just plotted the 
      point (xi, yi)

      Which means that the line is within yi+/- 1/2 
      

We need to be able to choose between yi+1 = yi and yi+1
      

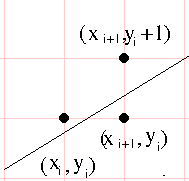To do this, we compute the distance between the actual y value and
the two pixel based y values.

      y = m(xi+1)+b

      d1 =  y - yi
         = m(xi+1)+b -yi

      d2 = yi +1 - y
         = yi +1 -(m(xi+1)+b)
      

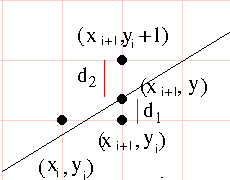      remember xi+1 = xi+1

We form a predictor, Pi for step i
     Pi = d1 - d2

     if Pi is positive, d1 is larger and the actual 
         point is closer to (xi+1, yi+1).
     if Pi is negative, d2 is larger and the actual 
         point is closer to ((xi+1, yi),

so d1 - d2 = m(xi+1)+b -yi - [yi +1 -(m(x+1)+b)]
           = 2(m(xi + 1) + b) - 2yi -1
           = 2m(xi + 1) - 2yi + 2b - 1
	   = 2mxi - 2yi + 2b + 2m -1

Remember m = Δy/Δx

This has a floating point computation hidden in m so let
       pi = Δx Pi

       The sign of pi and Pi are the same, which
       is what we are interested in.

       pi = Δx(d1 - d2)
       pi = 2Δyxi - 2Δx yi + Δx(2b +2m -1)
           let c =  Δx(2b +2m -1)
       pi = 2Δyxi - 2Δx yi + c

       Notice that this is an integer computation.

       so we can compute pi  and look at the sign to determine
       the value of yi+1

We don't want to recompute pi every 
iteration of the loop, it involves two multiples and two adds.
   
       Frequently this is solved by computing the amount pi 
       changes each step.

       pi  = 2Δy xi - 2Δx yi + c
       pi+1= 2Δy xi+1 - 2Δx yi+1 + c
       Δp = pi+1 -pi
          = 2Δy xi+1 - 2Δx yi+1 + c -[2Δy xi - 2Δx yi + c]
	  = 2Δy(xi+1-xi) 
	       - 2Δx (yi+1- yi) +c - c
        
	And we know that xi+1 = xi + 1 so,
	Δp= 2Δy(xi+1-xi) 
	       - 2Δx (yi+1- yi) +c - c
          = 2Δy - 2Δx (yi+1- yi) 

	Finally, if y did not change (ie pi < < 0) then
	    pi+1 = pi
	so Δp = 2Δy - 2Δx(yi-yi)
	      = 2Δy
  
        If y did change pi+1 = pi +1 
	and Δp = 2Δy - 2Δx(yi + 1 -yi)
	      = 2Δy - 2Δx

        To save computation, we can let 
	   A = 2Δy
	   B = - 2Δx

        And have the following code:
	     
        dx = this.x2 - this.x1;
dy = this.y2 - this.y1;
d = 0;
y = this.y1;
A = -2*dx;
B = 2*dy;
for(x = this.x1; x <= this.x2; x++) {
    this.PlotPoint(x,y);
    if (d >= 0) {
         d += B;
         y++;
    }
    d += A;
}