Deriving the Orthographic Projection

• Remember glOrtho(left, right, top, bottom, near, far) specifies the view volume.
• 
• We want to transform this to the cube (-1,-1,-1), (1,1,1)
• 
• It would be easiest for us to first translate the view volume to be centered on the origin.
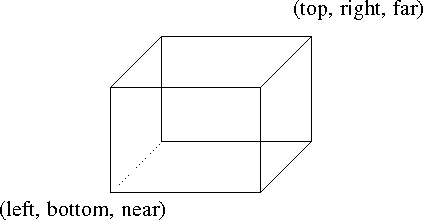
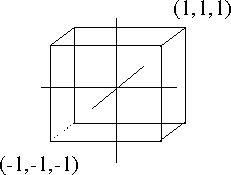
  • Focus on the x coordinate.

  • 
    The center is  left+1/2 width
    
    The width of the view volume is 
        (right-left) 
    
    So 1/2 of this, the distance from the left endpoint to the center  is
       (right-left)/2 
    
    So the center of the x distance is 
    
      cx = left + 1/2(right-left)
         = 2/2left + 1/2(right-left)
         = 1/2(2left + right - left)
         = 1/2(left+right)
         

• The case for y and z is similar
  • c_x = 1/2(right+left)
  • c_y = 1/2(top+bottom)
  • c_z = 1/2(far+near)
  • Or the transformation matrix T, where

        | 1 0 0 -cx |
        | 0 1 0 -cy |
    T = | 0 0 1 -cz |
        | 0 0 0  1  |
    	 

• After this transformation we have
• 
• Now we need to scale to the given volume
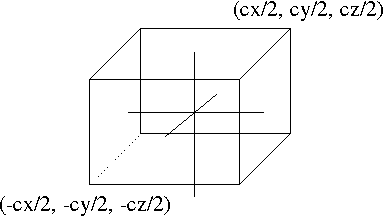
  • Note the volume is 2 x 2 x 2
  • If we need to, we could scale this to 2 x 2 x 1
  • Again, focusing on the x axis

    The current width is 
         right-left
    
    If we multiply by 1/(right-left)  the length will become 1.
    
    We want to divide by 1/2 that so
    
       sx =  1/(right-left)/2
                     = 2/(right-left)
     
    	  

  • Again the argument holds for y and z.
  • s_x = 2/(right-left)
  • s_y = 2/(top-bottom)
  • s_z = 2/(far-near)
  • Or the transformation matrix S, where

        | sx 0 0 0 |
        | 0 sy 0 0 |
    S = | 0 0 sz 0 |
        | 0 0 0  1 |
    	  

• Remember
  • the Camera is along the positive z axis in viewing coordinates
  • But the objects are along the positive z axis in modeling coordinates.
  • So we want to scale by (1,1,-1) to swap the x axis.
  • So S becomes S':

        | sx 0  0 0 |
        | 0 sy  0 0 |
    S'= | 0 0 -sz 0 |
        | 0 0  0  1 |
    	  

• So our projection matrix will be S'T

       | sx 0  0 0 | | 1 0 0 -cx |   | sx 0  0 sx(-cx) |
       | 0 sy  0 0 | | 0 1 0 -cy |   | 0 sy  0 sy(-cy) |
  S'T= | 0 0 -sz 0 | | 0 0 1 -cz | = | 0 0 -sz sz(-cz) |
       | 0 0  0  1 | | 0 0 0  1  |   | 0 0  0  1      |
  	  

• Again focusing on x

  • sx 0  0 sx(-cx) =  2/(right-left) (-1/2)(right+left) 
    	 = -(right+left)/(right-left)
    	 = (right+left)/(left-right)
    	 

  • And the final matrix is

    
      |      2                     right+left |
      |  ----------   0       0    ---------- |
      |  right-left                left-right |
      |                                       |
      |               2            top+bottom |
      |      0    ----------  0    ---------- |
      |           top-bottom       bottom-top |
      |                                       |
      |                       2      far+near |
      |      0        0   --------   -------- |
      |                   near-far   near-far |
      |                                       |
      |      0        0       0         1     |
    	 

• The final stage is the projection.
  • In the orthographic projection, this is just drop the z coordinate.
  • That matrix is

    | 1 0 0 0 |
    | 0 1 0 0 |
    | 0 0 0 0 |
    | 0 0 0 1 |
    
    	

• An example program:
  • void glGetFloatv(GLenum pname, GLfloat * params);
    • Part of a family of routines that allows you to get information from the OpenGL state machine.
    • We are particularly interested in finding the Projection matrix.
    • Pass the constant GL_PROJECTION_MATRIX,
    • And a pointer to 16 GLfloats.
    • You can query for many different things. (Look at the man page)
  • The return value is in column major form
    • OpenGL is column major,
    • you are used to row major.
    • No big issue, just reverse the loops.
    • See the example program
  • void glLoadMatrixf( const GLfloat *m)
    • Replace the current matrix with the given matrix.
    • Remember this is column major.