Line Drawing Algorithms

• This is a rasterization technique, we know the exact pixels we will be drawing on.
  • Both endpoints of the line are in raster coordinates.
  • and we will draw these endpoints.
• We want to find the way to fill in between these two endpoints.
• Why not y=mx+b?
• If dx = 0, or dy =0, the line drawing is trivial.
• DDA
  • Digital Differential Analyzer
  • Based on a technique from the 19th century
  • Assume the slope is between -1 and 1
    • What does this mean?
    • Can we test for this easily?

  • DDA (int x1, int y1, int x2, int y2)
    
     int x
     float y = y1
     float m = (y2-y1)/(x2-x1)
     for(x = x1; x≤ x2; x+= 1)
        plot(x, round(y))
        y += m
     plot(x2,y2)
     plot(x1,y1)
    
             

  • Does this work?
  • Is it efficient? (Does it draw any extra points)
  • What would we do to if |m| > 1?
  • How expensive is this?
• The problem with DDA is that is is all floating point.
  • What could we eliminate as floats? What do we need to keep as floats?
  • Floats are MUCH more expensive than ints
• Bressenham's Algorithm avoids floats
  • Start at the left end.
  • While not to the right end
  • Move along the major axis of change and decide to increment or not along the minor axis of change.
• Assume that pixel (i,j) has just been selected and 0 < m < 1
  • The actual value of y at this point is closer to j than to j-1 or j+1
  • He says : j-1/2 ≤ y ≤ j+1/2
  • The next pixel (i+1,j') will either be (i+1, j) or (i+1, j+1)
  • Because of the limit on the slope, we know that for the next point
  • j-1/2 < j' < j+3/2
• So representing the line as an equation

      y-y1 = m(x-x1)         m = Δy/Δx
  Substituting in for m and multiplying through by Δx we get
      (y-y1)Δx = (x-x1)Δy    Δx = x2-x1, Δy = y2-y1
      yΔx - xΔy -y1Δx + x1Δy  = 0
  partially expanding some Δx and Δy
      yΔx - xΔy -y1(x2-x1) + x1(y2-y1)  = 0
      yΔx - xΔy -y1x2 +y1x1 + x1y2 -x1y1  = 0
      yΔx - xΔy -y1x2 + x1y2  = 0    let x1y2-y1x2  = c
      yΔx - xΔy + c  = 0   
  
  D'(i,j) = jΔx - iΔy + c
      

  • Note,
    • if D'(i,j) = 0, then the point (i,j) is on the line.
    • if D'(i,j) < 0, then the point (i,j) is below the line.
    • if D'(i,j) > 0, then the point (i,j) is above the line.
  • We can let D(i,j) = 2D'(i,j) = 2yΔx - 2xΔy + 2c
    • This will not change the sign test above.
    • And it will eliminate j+1/2 to come later!
  • At point (i,j), evaluate D(i+1, j+1/2)
    • If D(i+1, j+1/2) < 0
      • The 1/2 point is below the line, so we need to move up.
      • Select (i+1, j+1) as the next point.
      • 
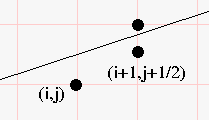
    • If D(i+1, j+1/2) > 0
      • The 1/2 point is above the line, no need to move
      • Select (i+1, j) as the next point.
      • 
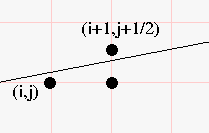
    • If they are the same, pick at random.
    • So given a point, we can predict if we need to move up or not,
    • But it is probably not best to re-evaluate D(i+1, j+1/2) every time.
    • Fortunately, we can derive a way to increment The value
      • If D(i+1, j+1/2) > 0, then we keep j the same, and move to the next point and evaluate D(i+2, j+1/2)

        • D(i+2, j+1/2) = 2(j+1/2)Δx - 2(i+2)Δy + 2c
                        = 2(j+1/2)Δx - 2iΔy - 4Δy + 2c
                        = 2(j+1/2)Δx - 2iΔy - 2Δy - 2Δy + 2c
                        = 2(j+1/2)Δx - 2(i + 1)Δy +2c  - 2Δy 
          	      = D(i+1, j+1/2)  - 2Δy
          	    

        • So the difference is just -2Δy
      • If D(i+1, j+1/2) ≤ 0 , we will increment j and want to evaluate D(i+2, j+3/2)

      • D(i+2, j+3/2) = 2(j+3/2)Δx - 2(i+2)Δy + 2c
                   2(j+3/2)Δx = 2jΔx + 3Δx
        	                    = 2jΔx + Δx + 2Δx
        			    = 2(j+1/2) Δx + 2Δx
        SO
        D(i+2, j+3/2) = 2(j+1/2)Δx - 2(i + 1)Δy +2c + 2Δx - 2Δy 
                      = D(i+1, j+1/2) + 2Δx - 2Δy 
        	    

      • Or, given if we increment y or not, we know how to increment the difference.
      • We need to find a starting point for D

        D(x1+1, y1+1/2) = 2yΔx - 2(x+1)Δy + 2c    
                      = 2(y1+1/2)Δx - 2(x1+1)Δy +  2(x1y2 - x2y1)
                      = 2y1Δx + Δx - 2x1Δy - 2Δy +  2x1y2 - 2x2y1
                      = 2x2y1 - 2x1y1 - 2x1y2 + 2x1y1 + 2x1y2 - 2x2y1 + Δx - 2Δy
                      = 2x2y1 - 2x2y1 - 2x1y1 + 2x1y1 - 2x1y2 + 2x1y2 + Δx - 2Δy
                      = Δx - 2Δy
        	    

    • So finally we have an algorithm

      Bressenhams(x1, y1, x2, y2)
      
       int y = y1
       int dy = y2- y1
       int dx = x2- x1
       int diff1 = -2dy
       int diff2 = diff1 + 2dx
       int D = dx - diff2
       for(int x=x1; x ≤ x2; x++)
           plot(x,y);
           if D > 0
               D+= diff1
           else
               D+= diff2
               y++