- -w ≤ x ≤ w
- -w ≤ y ≤ w
- -w ≤ z ≤ w
- We will clip against a rectangle (xmin,ymin) to (xmax, ymax)
- In application planning (ie between "zones")
- In the application to reduce points in the hardware.
- Anyplace in the pipeline.
- Before fragments is good, this will eliminate data.
- There are four cases for line segments:
- Both endpoints are within the clip window, so the line is accepted. (AB)
- One endpoint is inside and the other is outside, so the line must be clipped once. (CD)
- This is called shortening in our book.
- Both endpoints are outside the window and the line DOES NOT pass through the window, so the line is discarded. (EF)
- Multiple cases of this.
- Both endpoints are outside the window, but the line passes through the window, so the line must be clipped twice. (GH)
- The Cohen-sutherland clipping algorithm
- This algorithm tells us if we need to clip a line segment, accept it or reject it.
- It might be repeated for the line up to four times.
- use a bitcode bymaxbyminbxmaxbxmin
- Called an outcode
- For a point (x,y)
- bymax = 1 if y > ymax, 0 otherwise.
- bymin = 1 if y < ymin, 0 otherwise.
- bxmax = 1 if x > xmax, 0 otherwise.
- bxmin = 1 if x < xmin, 0 otherwise.
-
1001 | 1000 | 1010 ------------------ 0001 | 0000 | 0010 ------------------ 0101 | 0100 | 0110
- For a line, compute o1 and o2 for each endpoint of a segment. (very quick)
- if o1 = o2 = 0 then the segment is fine, no clipping is required.
- if o1 ≠ o2 but one is zero: clip one endpoint.
- This may require two intersections (against x and y)
- After the first clip, we can compute the outcode of the new point and check again.
- If o1 & o2 ≠ 0 both endpoints are on the same edge of the clipping window and the segment can be discarded.
- Otherwise ( o1 & o2 = 0) Both endpoints are outside of different edges of the window and we need to clip.
- The outcodes tell us what side we must clip against.
- if o1 ≠ o2 but one is zero: clip one endpoint.
- How will we clip?
- working with y=mx+b is problematic for vertical lines
- And is not really the tool we need.
- Parametric equations are a set of equations that express a set of quantities as explicit functions of a number of independent variables (or parameters) (Wolfram.)
- for a circle
- x = r cos(Θ)
- y = r sin(Θ)
- For a sphere:
- x = r cos(Θ)sin(φ)
- y = r sin(Θ)sin(φ)
- z = r cos(φ)
- In each of these, r is usually fixed (the radius) and Θ and φ are varied.
- Interesting shapes can be found by regularly varying r as well.
- For a segment from P1 to P2
- x(α)= (1-α)x1+αx2
- y(α)= (1-α)y1+αy2
- 0 ≤ α ≤ 1 for points on the line segment
- For a given value of α, we can compute the corresponding point.
- Liang-Barsky Clipping
- Use the fact above along with:
- If α > 1 it is past the right/top endpoint
- If α < 0 it is before the left/bottom endpoint.
- We can compute α for a line at a given window edge value:
- α = (ymax-y1)/(y2-y1)
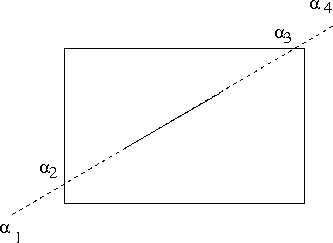
- Let
- α1 be the point where the line intersects the window y min.
- α2 be the point where the line intersects the window x min.
- α3 be the point where the line intersects the window y max.
- α4 be the point where the line intersects the window x max.
- If α1 ≤ 0 and α2 ≤ 0 and α3 ≥ 1 and α4 ≤ 1, then the line is accepted.
-
- If 0 < α1 <1 and α2 < 0 and α3 ≥ 1 and α4 ≤ 1
-
- Clip at α1, Why?
- Similar for the four other cases.
-
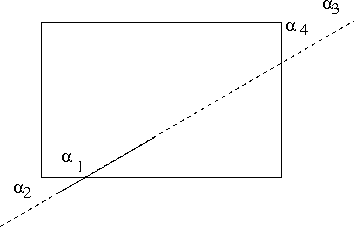
- If 0 < α1 < 1 and 0 < α2 < 1 and α3 ≥ 1 and α4 ≥ 1, then clip the line at α2. (Why? α1 < α2)
-
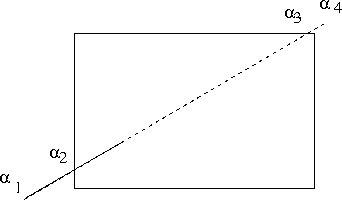
- Give a situation where α1 > α2 but all other conditions are met.
- This is true for the semetric classes as well.
-
- Assume 0 < α1 < α2 <α3 < α4 < 1
-
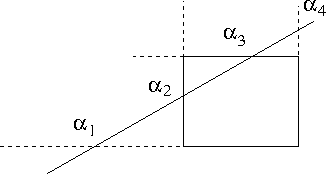
- Then the points to clip at are α2 and α3
-
- Assume 0 < α1 < α3 <α2 < α4 < 1
-
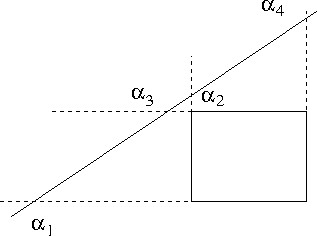
- Then the line can be trivially rejected for two reasons, (WHY?)
- this is the case where the line is completely above. and to the left of the clip box.
-
- Use the fact above along with: