Viewing

• Number 1: OpenGL is a dimensionless system.
  • A coordinate system exists, however no units have been assigned to that system.
  • It is up to us to do so.
• Number 2: OpenGL is a very flexible viewing system
  • There is no single camera, lens, ... or other restriction.
• In the end, we need to map a 3d image to a 2d surface.
  • Or with current technology, to two different 2d surfaces, drawn from a slightly different position, delivered to each eye.
• The red book describes the viewing process in 5 steps.
  1. Position the camera to the location from which you wish to shoot your picture.
  2. Move the jusbject to be photographed into the desired location.
  3. Pick a lens for the camera and adjust the lens.
  4. Take the picture
  5. Shrink or stretch the resulting image to fill your photo paper
• Step 1 is seting up the viewing transformation
  • We model the camera and the scene in model coordinates
  • And we need to make this the center of projection (COP), or move it to the origin.
  • So we need to do a transformation from one coordinate system to another.
  • The camera position is usually specified by three quantities.
    • The camera position (eye_x, eye_y,eye_z)
    • The lookat position (center_x, center_y, center_z)
    • These two quantities give us a vector, which we will call the view normal.
    • LOOKAT = center- eye
    • Next we need an up position (up_x, up_y, up_z)
    • 
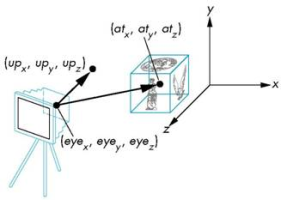
    • (Stolen from a web page, but ultimately from our book)
    • With the UP position, we can compute an up vector (UP = up-lookat)
    • We will now use the Cross Product of two vectors.
      • u × v
      • Returns a vector normal to u and v.
      • Look at cross in vec.h
      • One of the nice properties of the cross product, is that u × v is normal to both u and v.
    • So now we can compute a right vector.
    • RIGHT = LOOKAT × UP
    • But we might not trust the up vector to be completely correct, so we frequently do an additional cross product UP' = LOOKAT × RIGHT
    • If we normalize LOOKAT, UP, RIGHT
  • The system we just formed, LOOKAT, RIGHT, UP' forms a basis for a vector space.
    • If we want to change from our modeling vector space to our viewing vector space, we need to do a change of baisis.
    • This is just a matter of using the system we just developed as a transformation matrix.
    • Look at LookAt in mat.h
    • This will form a matrix which will place the camera at the origan.
  • There are other methods of specifying this position (See section 4.3.2 - 4.3.4)
• Step 2
  • They mention that this is just doing step 1 in a different order.
  • But it can be more that that.
  • In my case, I want to move the object I am drawing into a "good" position.
  • And possibly perform transformations on it as time goes by.