Navigation Meshes

This is based on Introduction to AI with Blueprint
- You will be doing this for your next assignment.
- It is really good and I feel the results are worth it.
  - You end up with a NPC who can chase you, look for food, run to random locations or hide
- He does a nice job integrating some theory as well.
- This goes very fast and is very in depth so I thought a preview might be in order.
Some Ideas.
- An Intelligent Agent or IA is an autonomous entity that acts
- In this case, he says that there are three components
  - Sense or discover what is in the environment.
  - Think or figure out what to do next based on the input.
  - Act or take an action based on the action.
Navigation Meshes
- This is a reasonably modern concept.
- Build a mesh of convex polygons that "covers" the areas where we can navigate.
- In (A navigation mesh for dynamic environments ) they present this navigation mesh for "Zelda" A navigation mesh for dynamic environments
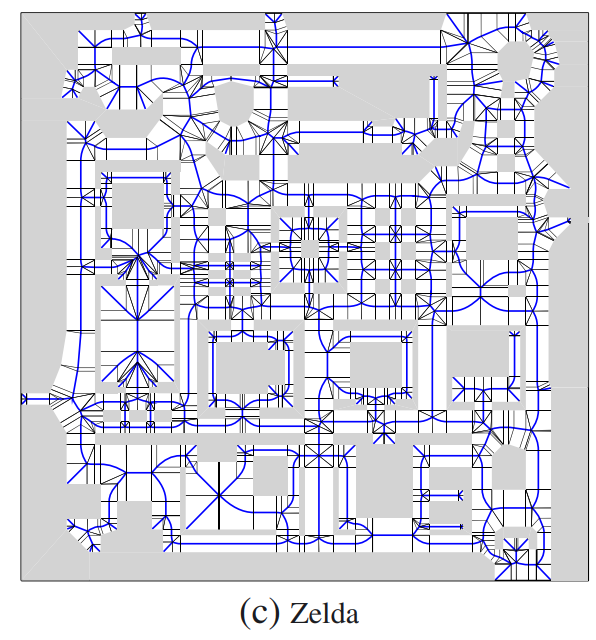
- I grabbed this one from Gamedev.net.
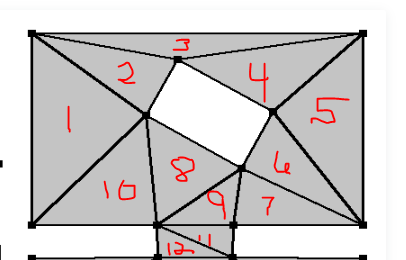
- Navigation within a polygon is simple since it is convex, just move directly there.
- Navigation outside of polygons, form a graph and do a shortest path computation (Algorithms or Discrete II)

Building a nav mesh is easy,

just drag a Nav Mesh Bounds Volume into the scene
There are some parameters you might need to adjust
But this will generate the mesh for you.
He cautions about large nav meshes.
You can stitch multiplies together if you wish.
- There are functions like GetRandomReachablePointInRadius
  - He employs this to make the NPC move about in the scene.
The next item is the AI controller
- Remember a character is a pawn that moves around.
- These can be controlled by a controller.
- You will probably have a controller for each different type of NPC in your scene.
- He uses the controller for two things.
  - To run the AI, which controls the character (NPC)
  - To implement functions which communicate between the character (NPC) and the AI.
Nav Mesh Properties
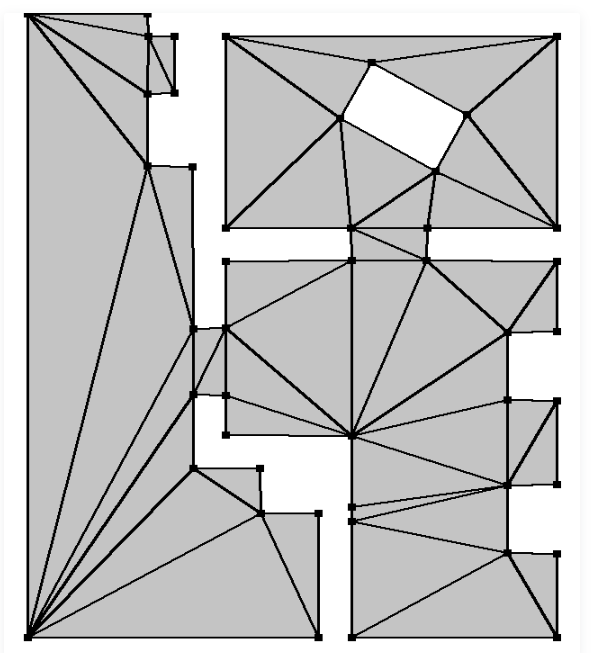
- Nav meshes are constructed from convex polygons (most likely triangles, ask any graphics student.
- Convex means you can get from any point in a polygon to any other point via a straight line.
- So navigation between points inside a polygon is easy.
But how does this work.
- Becomes

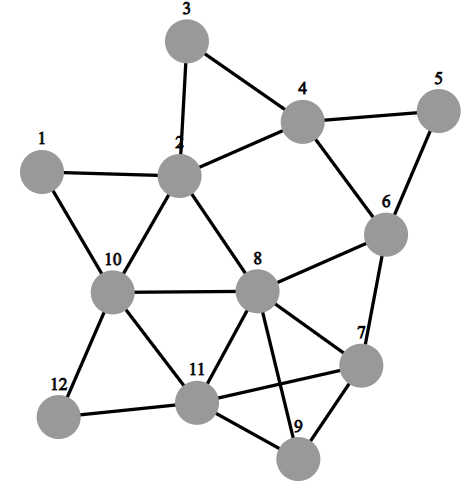
We can now run any graph algorithm.

BFS (Breadth First Search)


 BFS(G, start, end)
   done ← false
   Set all v.found to false.
   start.found ← true
   start.parent ← NULL 
   Q.enqueue(start)
   while not done and not Q.isEmpty()
      n ← Q.Dequeue()
      if end = n 
          done ← done
      for v in n.adjacent()
         if  not v.found
            v.parent ← n
            v.found ← true
            Q.enqueue(v)

This is probably good if there are no costs.
But it explores all directions.

Dijkstra's is good if there are associated costs

Dijkstras(G, start, end)

 done ← false
 Set all v.found to false
 Set all v.dist to ∞
 start.found ← true
 start.dist ← 0
 start.parent ← NULL
 Q.enqueue(all v)          // note this is a heap
 while not Q.empty and not done
     n ← Q.dequeue    // get item with lowest cost.
     if n = end
        done ← true
     for each v in n.adj
        if n.dist  + dist(n,v) < v.dist and not v.done
            v.dist ← n.dist + dist(n,v)
            v.parent ← n

Not the best for pathfinding
By Subh83 - Own work, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=14916903

A* is an improved algorithm.

It can be considered an extension to Dijkstra's
This works on weighted graphs as well
But it uses a heuristic to predict where to go next.
In our case, the euclidian distance will do.

A*(G, start, end);

 done ← false
 Set all v.found to false
 Set all v.dist to ∞
 start.found ← true
 start.dist ← 0
 start.approx ← 0
 start.parent ← NULL
 Q.enqueue(start)          // note this is a heap
 while not Q.empty and not done
     n ← Q.dequeue    // get item with lowest approximated.
     if n = end
        done ← true
     for each v in n.adj
        if n.dist  + dist(n,v) < v.dist and not v.done
            v.dist = n.dist + dist(n,v);
            v.approx ← v.dist +  ApproxDist(v, end); 
            v.parent ← n
            Q.enqueue(v)

ApproxDist(v, end) 

 Return an approximation of the distance from the v to the end.

By Subh83 - Own work, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=14916867