Boolean Expressions

• Boolean algebra was invented by George Bool
• Built from the operations (and, or not)
  • aandb, (ab)
  • aor b, (a+b)
  • not a , a'
• truth table
  • Give truth table for f(x,y,z) = xy + xz' + x'yz
  • In general, we will work the other way, given a truth table find the function.
• Properties
  • 1a = a, 0+a = a
  • 0a = 0, 1+a = 1
  • aa = a, a+a = a
  • aa' = 0, a+a' = 1
  • ab = ba, a+b = b+a
  • (ab)c = a(bc), (a+b)+c = a + (b+c)
  • a(b+c) = ab + ac
  • (ab)' = a'+b', (a+b)' = a'b' (demorgans law)
  • (a')' = a
• Use a truth table to prove one form of demorgan's law
• Use a truth table to disprove (ab)' = a'b'
• Given an expression, it is often desirable to simplify that expression
  • F(x,y,z) = xyz + xyz'+x'y, simplify
• Truth tables and functions are in some way equivilent.
• All boolean expressions can be represented as a sum of products
  • t₁ + t₂ + t₃ + ... + t_n
  • We will take advantage of this later on.

Basic Gates

• Combinational Circuits
• Sequential Circuits
• Look at and, or not in tkgate.
• xor, ab'+a'b
• universial gates
  • nand, nor, not
  • Derived in terms of transistors
  • not
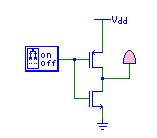
  • nor
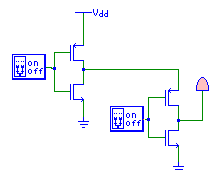
  • Three and more input gates can be formed as well
  • the tkgate file
• Gate delay
  • not is almost free
  • and and or are the basic unit of time
  • xor is more complex
  • Show probes, and timing in tkgate
  • Show shortcut for negation
  • Show circuit for x+y'z