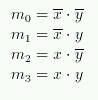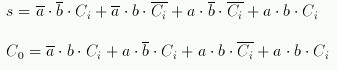Karnaugh Maps

• Minterms -
  • Consider the folowing table:

  • x	y	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15
    0	0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
    0	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
    1	0	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
    1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

  • This table represents all possible circuits for two bits.
  • The terms F₁, F₂, F₄, and F₈ are somehow interesting.
    • These are called minterms
    • We can build any other expression from them
    • xy = F₈
    • x+y = F₂+F₄+F₈
    • F₁₁ = F₁+F₂+ F₈
    • Change the notation F₁ = m₀, F₂ = m₁, F₄ = m₂, F₈ = m₃
    • 
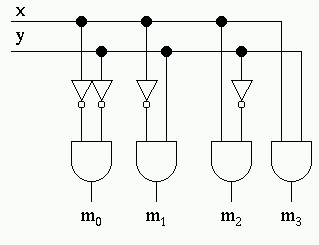
    • Note, that in general, the subscripts for minterm indicate the bit pattern for that minterm.
    • 
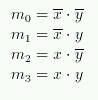
    • This observation holds true for minterms with more inputs.
    • A full adder

      a	b	Ci	s	Co
      0	0	0	0	0
      0	0	1	1	0
      0	1	0	1	0
      0	1	1	0	1
      1	0	0	1	0
      1	0	1	0	1
      1	1	0	0	1
      1	1	1	1	1

    • s = m₁+m₂+m₄+m₇
    • C_o = m₃+m₅+m₆+m₇
    • 
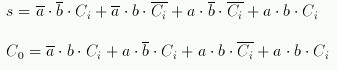
    • Do these results match what we got with algebraic manipulation?
  • We want to make sure that our expressin is a simple as possible.
  • To do this for circuits of 4 inputs or less, we can use a Karnaugh Map.
    • 
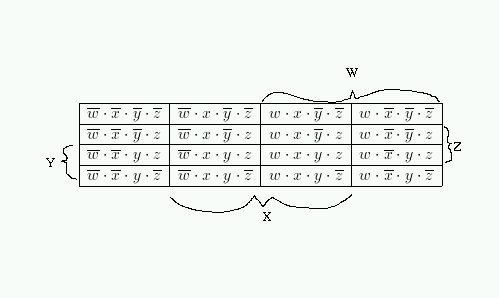
    • We next place a 1 on the map for each term that is in the equation.
    • For C_o above

      	1
      1	1
      	1

  • Circle the adjacient pairs
  • 
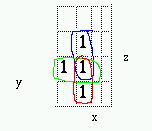
  • Read the terms that remain constant for circled pairs.
  • 
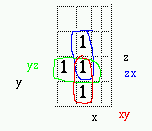
  • So C_o = xy+yz+xz
  • Prove this.
  • There is more involved than this, but this will do to illustrate the principal.