Midterm Exam, CSCI 312, Fall 2017

• Make sure you answer each question completely and thoughtfully.
• Please make sure your answers are clearly labeled with the question number.
• Please write neatly and make any diagrams as neat as you can. If I can't read it, it is wrong.
• Point values are listed by each question.

1. [6 points] Draw a diagram that represents the WOMBAT CPU. Label all parts.
   
   This, in my opinion, should have been 12% free credit on the test.

2. Fetch-Decode-Execute
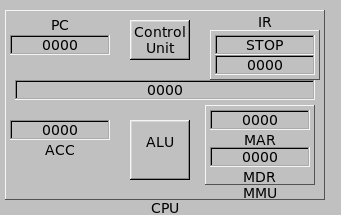
   1. [6 points] Describe what happens at each phase of the Fetch-Decode-Execute cycle.
      The fetch portion of consists of fetching the data stored at the address contained in the program counter and storing it in the instruction register.

      In the decode portion the control unit examines the op-code of the instructon stored in the IR to decide what actions are required.

      In the execute phase, the control unit sends signals to the other units within the CPU which facilitate the execution of the instruction.

      The instruction is fectch from memory, decode and executed is an ok answer for CSCI 125 but given the time spent on this so far in this class, it is totaly insufficient.

      I feel you really should reference the figure you have just drawn in your discussion.

   2. [4 points] Using RTN, describe at a component level what occurs during the Execute phase of a WOMBAT add instruction.

      BUS ← IR
      MAR ← BUS
      MDR ← M[MAR]
      BUS ← MDR
      ALU OP:  ACC + BUS
      ACCC ← ALU
             

      Given the homework you have done, I really expected this to be another 20% of the test which could be done accurately and quickly.

      PC → BUS as the first step is wrong in 2 out of 3 portions.

3. [4 points] Registers
   1. What is a special purpose register? Give an example of a special purpose register in the WOMBAT architecture.

      A special purpose register is a register which is used for a specific (or special) purpose. The following registers in wombat are special purpouse: PC, IR, MAR, MDR, INReg, OUTReg.

   2. What is a general purpose register? Give an example of a general purpose register in the WOMBAT architecture.
      A general purpose register is a register that the programmer can use for any purpose. More specifically any data can be stored in a general purpose register. In wombat the ACC is a general purpose register.
      Memory is not a register but a register could be considered memory.

      The register file is a collection of registers, it is not a single register.

      The ALU is NOT a reigster. No way no how.

      ADD, ADDI, ... are INSTRUCTIONS not registers.

4. [8 points] The authors of our book describe four factors that affect CPU performance. Name each and describe how it affects the performance of a program.
   Open your book to page 39. Commit these to memory. You were told multiple times to do so in both the notes and in class. You did multiple exercises relating to this.

5. [2 points] A CPU has a clock that runs at 2.0 GHz. Assume the CPI for this machine is 1. How long does it take to execute a single instruction. Please give your answer in proper units. Please show all work.

   2GHz = 2x109 cycles/ 1 second.
   But in this question we want time so start with
   
      1 second         1 cycle
   ------------- x -------------- = .5 x 10-9 seconds/instruction
   2 x 109 cycles   1 instruction
   
   or 500x10-12 seconds x 1012 ps / sec = 500ps.
   
   The answer is 500ps.
       

   Again, I think this should have been free points.

   If you told me 2GS/cycle think for a moment, that is about 63 years. Are you willing to wait your entire life for a single instruction or two?

6. A processor, running at 2GHz, has three classes of instructions with characteristics for a given program listed in the table below.

   Class	CPI	Frequency
   A	1	20%
   B	2	20%
   C	4	60%

   1. [2 points] Compute the average CPI for this machine.
      1 x .2 + 2 x .2 + 4 x .6 = .2 + .4 + 2.5 = 3 The average CPI is 3.

   2. [2 points] If the program requires 2x10⁹ instructions, how long will it take to execute this program.

        1 second         3 cycles        1x109 instructions 
      ------------- x  ------------- x  ------------------- = 3 sec/prog
      2 x 109 cycles   1 instruction         1 prog
      	

   3. [2 points] A programmer has written an optimizer for the compiler that will reduce the frequency of instructions in class C to 40% but increase the frequency of instructions in class A and B to 25% and 35% respectively. In addition, the number of instructions required for the program will change to be 2.3x10⁹. Should you use this compiler optimization and why? Show all work and an unsupported answer is wrong.

      
       1 x .25 + 2 x .35 + 4 x .4 = .25 + .7 + 1.6 = 2.55
       NEW CPI = 2.55
      
        1 second       2.55 cycles       2.3x109 instructions 
      ------------- x  ------------- x  --------------------- = 2.93 sec/prog
      2 x 109 cycles    1 instruction         1 prog
      	

      Since the new compiler produces a faster program it should be used.
7. For a 4 input MUX
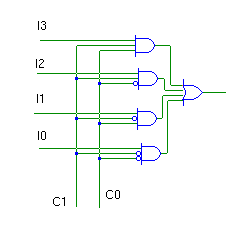
   1. [4 points] Describe the input, output and function of this MUX.

      	There are four data input lines.
      	There are two control input lines.
      	There is a single output line.
      	The value of the control line is used to select a single input line to pass through to the output.  Assume control has a value of 0 ≤ n ≤ 3, then input line n will be output.  
      	

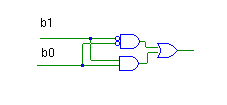
   2. [2 points] Draw a circuit to implement this MUX.
      

8. [6 points] Design and implement a circuit which takes two bits as input and adds a third bit such that the number of 1s in the three bits is always odd. Your answer should include a truth table, an equation and a circuit.

   b1	b0	O
   0	0	1
   0	1	0
   1	0	0
   1	1	1

   O = b1·b0 + b1· b0